 |
Главная |
Примеры решения типовых задач
|
из
5.00
|
Пример 1. Разложить в ряд Фурье периодическую (с периодом  ) функцию
) функцию  , заданную на отрезке
, заданную на отрезке 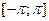

Решение. Рядом Фурье функции  называется функциональный ряд вида
называется функциональный ряд вида

где коэффициенты  определяются по формулам
определяются по формулам
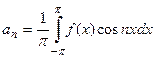 ,
,  .
.
Так как заданная функция кусочно-монотонная и ограниченная на отрезке  , то ее ряд Фурье сходится в любой точке
, то ее ряд Фурье сходится в любой точке  . Вычислим коэффициенты этого ряда:
. Вычислим коэффициенты этого ряда:

 ,
,





Подставляя найденные коэффициенты в ряд Фурье, получим

Пример 2. Разложить в ряд Фурье по косинусам функцию 

на отрезке  и найти сумму ряда
и найти сумму ряда 
Решение. Продолжим функцию четным образом и вычислим коэффициенты Фурье:



Следовательно, 
Полагая  , получаем:
, получаем:
 ,
,  .
.
Пример 3. Решить задачу Штурма-Лиувилля

Решение. Требуется найти отличные от тождественного нуля (нетривиальные) решения дифференциального уравнения
 удовлетворяющие краевым условиям
удовлетворяющие краевым условиям  . Те значения параметра
. Те значения параметра  , при которых существуют такие решения, называются собственными значениями краевой задачи, а соответствующие или нетривиальные решения – собственными функциями.
, при которых существуют такие решения, называются собственными значениями краевой задачи, а соответствующие или нетривиальные решения – собственными функциями.
Рассмотрим три случая:
1)  . Характеристическое уравнение
. Характеристическое уравнение  имеет два действительных корня
имеет два действительных корня  . Общее решение дифференциального уравнения в этом случае имеет вид
. Общее решение дифференциального уравнения в этом случае имеет вид
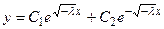 .
.
Удовлетворяя краевым условиям, приходим к системе

которая имеет действительное решение  и, следовательно,
и, следовательно, 
2)  . Общее решение дифференциального уравнения
. Общее решение дифференциального уравнения  и краевые условия снова дают
и краевые условия снова дают 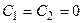 , а поэтому и в данном случае
, а поэтому и в данном случае 
3)  . Характеристическое уравнение имеет два мнимых корня
. Характеристическое уравнение имеет два мнимых корня  , которым соответствует общее решение дифференциального уравнения
, которым соответствует общее решение дифференциального уравнения 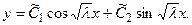 Для удобства перепишем это решение в виде
Для удобства перепишем это решение в виде  Из условия
Из условия 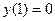 получаем
получаем  и поэтому
и поэтому  Условие
Условие  приводит к уравнению
приводит к уравнению  Так как
Так как  и
и  , то
, то  , откуда получаем
, откуда получаем 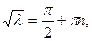
 . То есть, собственные значения задачи Штурма - Лиувилля
. То есть, собственные значения задачи Штурма - Лиувилля
 ,
,
а собственные функции
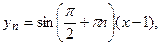
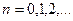 .
.
Пример 4. Методом Даламбера найти форму струны, определяемую волновым уравнением  , если в начальный момент времени ее форма и скорость удовлетворяют условиям Коши
, если в начальный момент времени ее форма и скорость удовлетворяют условиям Коши  ,
, 
Решение. Нетрудно проверить, что если 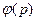 и
и 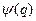 - любые дважды дифференцируемые функции, то функция
- любые дважды дифференцируемые функции, то функция  является решением волнового уравнения. Удовлетворяя начальным условиям, получим решение поставленной задачи в виде
является решением волнового уравнения. Удовлетворяя начальным условиям, получим решение поставленной задачи в виде

Подставляя сюда функции 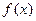 и
и 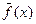 , имеем
, имеем
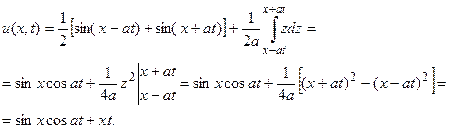
Следует отметить, что решение Даламбера, полученное для бесконечной струны, имеет практическое применение только для малых значений времени, когда колебания конечной струны не успели дойти до ее концов. Кроме того, функции  и
и  должны быть такими, чтобы в течение всего процесса
должны быть такими, чтобы в течение всего процесса  была малой величиной, которой можно пренебречь по сравнению с 1.
была малой величиной, которой можно пренебречь по сравнению с 1.
Пример 5. Методом Фурье решить смешанную задачу для волнового уравнения  на отрезке
на отрезке 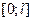 , если
, если

Решение. Данная задача называется смешанной, так как помимо начальных условий Коши, содержит краевые условия жесткого закрепления струны по ее концам (два последних условия).
Руководствуясь методом Фурье (методом разделения переменных), будем искать нетривиальные решения волнового уравнения, удовлетворяющие только краевым условиям, в виде произведения  . Подставляя
. Подставляя  в исходное уравнение, для функции
в исходное уравнение, для функции  получаем задачу Штурма-Лиувилля
получаем задачу Штурма-Лиувилля

Ее собственные значения 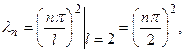
 . При этих значениях
. При этих значениях  решение поставленной задачи может быть представлено в виде суммы бесконечного ряда
решение поставленной задачи может быть представлено в виде суммы бесконечного ряда

где постоянные 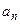 и
и  подлежат определению с помощью начальных условий. Их использование на отрезке
подлежат определению с помощью начальных условий. Их использование на отрезке  в общем случае дает
в общем случае дает


Так как в нашем случае  ,
, 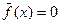 , то
, то  , а коэффициенты
, а коэффициенты 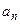 находим двукратным применением метода интегрирования по частям
находим двукратным применением метода интегрирования по частям


Окончательно,
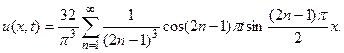
Колебания струны, происходящие по найденному закону, представляет собой суперпозицию колебаний, называемых собственными колебаниями или стоячими волнами. При таких колебаниях каждая точка x струны производит гармонические колебания с частотой, в общем случае, равной  и с амплитудой
и с амплитудой 
Пример 6. Найти решение смешанной задачи для уравнения теплопроводности  на отрезке
на отрезке  , удовлетворяющее начальному условию
, удовлетворяющее начальному условию  , если
, если

Решение. Применяя для решения уравнения метод разделения переменных и удовлетворяя краевым условиям, в общем случае получим
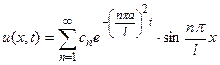 ,
,
где  - коэффициенты, подлежащие определению из начального условия. Удовлетворяя ему, имеем
- коэффициенты, подлежащие определению из начального условия. Удовлетворяя ему, имеем

откуда видно, что  являются коэффициентами Фурье при разложении функции
являются коэффициентами Фурье при разложении функции  в ряд по синусам на интервале
в ряд по синусам на интервале  , т.е.
, т.е.

Окончательное решение поставленной задачи может быть записано в виде
 .
.
В нашем случае  ,
,  и поэтому
и поэтому


Следовательно,
 .
.
Пример 7. Найти решение уравнения теплопроводности  для неограниченного стержня
для неограниченного стержня  , удовлетворяющее начальному условию, если
, удовлетворяющее начальному условию, если

Решение. В общем случае решение поставленной задачи Коши может быть найдено в виде интеграла Пуассона

Поскольку в нашем случае на отрезке 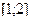 функция
функция  равна постоянной
равна постоянной  , а вне его температура равна 0, то решение примет вид
, а вне его температура равна 0, то решение примет вид

где  ,
,  ,
,  ,
, 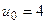 .
.
Данный результат, для упрощения вычислений, можно преобразовать к интегралу вероятностей (функции Лапласа)
 .
.
Для этой функции имеются специальные таблицы, приведенные в Приложении 3. Тогда
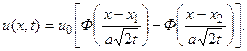
В нашем случае

Эта формула дает значение температуры в любой точке стержня x в любой момент времени  , если в начальный момент времени
, если в начальный момент времени  на участке
на участке  был произведен мгновенный нагрев стержня до значения 4. Например,
был произведен мгновенный нагрев стержня до значения 4. Например,  ,
,  , то
, то

Отметим, что рассмотренный подход к решению задачи теплопроводности целесообразен тогда, когда стержень настолько длинный, что температура в его внутренних точках в рассматриваемые моменты времени мало зависит от условий на его концах.
ЧИСЛЕННЫЕ МЕТОДЫ
|
из
5.00
|
Обсуждение в статье: Примеры решения типовых задач |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

