 |
Главная |
Примеры решения типовых задач
|
из
5.00
|
Пример 1. Дана таблица значений функции  . Построить для этой функции интерполяционный многочлен Ньютона и с помощью его найти приближенное значение функции для заданного аргумента
. Построить для этой функции интерполяционный многочлен Ньютона и с помощью его найти приближенное значение функции для заданного аргумента  .
.
| X | 3.50 | 3.55 | 3.60 | 3.65 | 3,70 | 
|
| Y | 33.115 | 34.813 | 36.598 | 38.475 | 40.447 | 3.57 |
Решение. Интерполяционный многочлен Ньютона для заданной функции имеет вид
 где
где  . Составим таблицу конечных разностей для заданных значений
. Составим таблицу конечных разностей для заданных значений

| 
| 
| 
| 
|
| 3.50 3.55 3.60 3.65 3.70 | 33.115 34.813 36.598 38.475 40.447 | 1.698 1.785 1.877 1.972 ------ | 0.087 0.092 0.095 ------ ------ | 0.005 0.003 ------ ------ ------ |
При составлении таблицы конечных разностей ограничиваемся разностями третьего порядка, так как они практически постоянны. Поэтому в формуле Ньютона полагаем  . Приняв
. Приняв  ,
,  ,
,  будем иметь:
будем иметь:

или

где 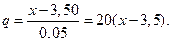 Подставим в выражение для
Подставим в выражение для  значение
значение  .
.
Получим  Тогда,
Тогда,

Следовательно, 
Пример 2. Дана таблица значений функции  . Используя метод наименьших квадратов, подобрать для заданных значений
. Используя метод наименьших квадратов, подобрать для заданных значений  и
и 
1) линейную функцию  ;
;
2) квадратичную функцию  .
.
Построить графики этих функций.
| X | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| Y | 0.31 | 0.82 | 1.29 | 1.85 | 2.51 | 3.02 |
Решение.
1) Аппроксимируем таблично заданную функцию  линейной
линейной  . Составим систему для определения
. Составим систему для определения 

Предварительно вычисляем  ,
,  ,
,  ,
,  Следовательно,
Следовательно, 
Решая эту систему, находим  и
и  :
:  ,
,  .
.
Искомый многочлен  .
.
2) Аппроксимируем таблично заданную функцию  квадратичной функцией
квадратичной функцией  . Составим систему для определения
. Составим систему для определения 

Предварительно вычисляем
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,  ,
,

Получим систему уравнений вида
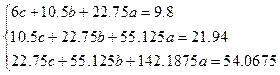
Решая эту систему, находим  :
:  ,
, 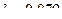 ,
,  .
.
Искомый многочлен 







Рисунок 2.14. Исходные данные и результаты аппроксимации
Пример 3. Получить приближенное решение системы методом простой итерации с точностью 0.01.

Решение. Выразим переменную  из i-го уравнения системы, получим
из i-го уравнения системы, получим

В качестве начального приближения возьмем совокупность чисел  ;
;  ;
;  . После первого шага получим:
. После первого шага получим:

После второго шага: 
Дальнейшие вычисления располагаем в таблице

| 
| 
| 
|
| 0 1 2 3 4 5 6 | 1.2000 1.2000 0.9640 1.0098 0.9975 1.0007 0.9998 | 0.0000 1.0600 0.9440 1.0104 0.9966 1.0009 0.9997 | 0.0000 1.1600 0.9480 1.0144 0.9960 1.0012 0.9997 |
Точное решение (  ) практически достигается на 6-ой итерации.
) практически достигается на 6-ой итерации.
Пример 4. Отделить корни и найти приближенное решение заданного уравнения с точностью  методом Ньютона (1) и методом итераций (2).
методом Ньютона (1) и методом итераций (2).
1) 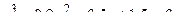 ; 2)
; 2)  .
.
Решение. 1)Локализуем корни первого уравнения. Обозначим  .
.
Применим метод Лагранжа. Найдем граничные значения интервалов  и
и  , которым принадлежат корни уравнения.
, которым принадлежат корни уравнения.
Найдем  . Верхняя граница
. Верхняя граница  положительных корней полинома
положительных корней полинома  вида
вида
f(x) = a0x n + a1xn-1 +... +akxn-k +…+ an , (a0 >0)
определяется по формуле Лагранжа :
 ,
,
где: k ³ 1 – меньший номер отрицательных коэффициентов полинома;
B – максимальный по модулю отрицательный коэффициент.
Таким образом,  ,
,  , k=1
, k=1
 =1,2
=1,2
Найдем  . Составим
. Составим  , получим
, получим  , а значит уравнение
, а значит уравнение  или
или 
 =1,145
=1,145
Найдем  . Составим
. Составим  , получим
, получим
 .
.  =1,365
=1,365
Найдем  . Составим
. Составим  , получим
, получим
 .
.  =1,333
=1,333
Таким образом, получим интервалы  и
и  , которым принадлежат корни уравнения, окончательно
, которым принадлежат корни уравнения, окончательно 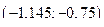 и
и 
Уравнение имеет действительный корень, лежащий в промежутке  . Уточним этот корень методом касательных, выбрав в качестве
. Уточним этот корень методом касательных, выбрав в качестве  .
.
Проверим условия:
1)  , т.е.
, т.е.  . Это условие выполняется, так как
. Это условие выполняется, так как 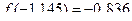 , а
, а  .
.
2)  . Это условие выполняется, так как
. Это условие выполняется, так как  ,
,  ,
, 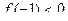 и
и  .
.
Для вычислений применяем формулу Ньютона

Для вычислений используем итерационную таблицу
| Номер итерации | 
| 
| 
| 
|
| 0 1 2 | -1 -0.949 -0.9464 | -0.2 -0.0093 -0.0004 | 3.9 3.5814 3.5657 | -0.051 -0.0026 -0.00001 |
Ответ:  .
.
2) Метод итераций. Отделяем корни графически. Уравнение  перепишем
перепишем  . Построим графики функций
. Построим графики функций  и
и 
Уравнение имеет действительный корень, лежащий в промежутке  .
.

Рисунок 2.15. Пример отделения корней графическим методом
Для уточнения решения методом итераций приведем уравнение к виду  . При этом должно выполняться условие
. При этом должно выполняться условие  для
для  . Функцию
. Функцию  будем искать из соотношения
будем искать из соотношения  , считая, что
, считая, что  , где
, где  число
число 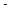 имеет тот же знак, что и
имеет тот же знак, что и  в промежутке
в промежутке  . Находим
. Находим  .
.
Так как  , то можно взять
, то можно взять  . Тогда
. Тогда

Пусть  , тогда
, тогда  . Вычисления расположим в итерационной таблице
. Вычисления расположим в итерационной таблице

| 
| 
| 
| 
|
| 0 1 2 3 4 5 | 0 -0.3 -0.3693 -0.3785 -0.3795 0.3796 | 0 0.09 0.1364 0.1433 0.1440 | 0 -0.027 -0.0504 -0.0542 -0.0546 | -0.3 -0.3693 -0.3785 -0.3795 -0.3796 |
Ответ:  .
.
Пример 5. 1) Вычислить интеграл.

по формуле трапеций с тремя десятичными знаками
2) Вычислить интеграл

по формуле Симпсона при n=8; оценить погрешность результата, составив таблицу конечных разностей.
Решение.
1) Для достижения заданной степени точности необходимо определить значение  так, чтобы
так, чтобы
 (*)
(*)
Здесь  ;
;  ;
; 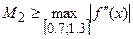 , где
, где  .
.
Находим  ,
,  ;
;
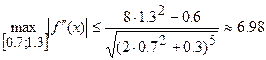 .
.
Положим 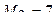 , тогда неравенство (*) примет вид
, тогда неравенство (*) примет вид  , откуда
, откуда 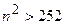 , т.е.
, т.е.  ; возьмем
; возьмем  .
.
Вычисление интеграла проводим по формуле
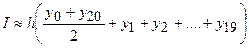 ,
,
где  ;
;  ;
;  .
.
Все вычисления приведены в таблице :

| 
| 
| 
| 
| 
|
| 0 1 2 3 4 5 6 7 8 9 10 | 0.7 0.73 0.76 0.79 0.82 0.85 0.88 0.91 0.94 0.97 1.00 | 0.88386 0.85572 0.82898 0.80366 0.77973 0.75700 0.73546 0.71501 0.69551 0.67700 0.65937 | 11 12 13 14 15 16 17 18 19 20 | 1.03 1.06 1.09 1.12 1.15 1.18 1.21 1.24 1.27 1.30 | 0.64259 0.62657 0.61140 0.59669 0.58272 0.56935 0.55658 0.54431 0.53253 0.52129 |
Таким образом,
 .
.
Ответ: 0,404
2) Согласно условию  , поэтому
, поэтому  .
.
Применим метод Симпсона, разобьем интервал  на четное число частей
на четное число частей  . Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла
. Каждая пара полосок ограничивается сверху параболой, проходящей через три точки. Затем вычисляется площадь каждой пары полосок, ограниченной сверху параболой. Сумма площадей всех пар полосок является приближенным значением определенного интеграла
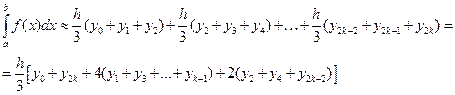
Расчетная формула имеет вид

где  ,
, 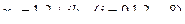 .
.
Вычисления значения функции запишем в таблице:

| 
| 
|
| 0 1 2 3 4 5 | 1.2 1.25 1.30 1.35 1.40 1.45 | 0.1211 0.1520 0.1782 0.2000 0.2176 0.2312 |
| 6 7 8 | 1.50 1.55 1.60 | 0.2410 0.2473 0.2503 |
Следовательно,
 .
.
Ответ: 0,88278
Пример 6 .Получить численное решение дифференциального уравнения  , удовлетворяющее заданному начальному условию
, удовлетворяющее заданному начальному условию  на отрезке
на отрезке  с шагом
с шагом  , методом Эйлера
, методом Эйлера
 ,
,  ,
,  .
.
Решение. Формула Эйлера для решения задачи Коши имеет вид

В нашем случае 

Находим последовательные значения аргумента:  ,
,  ,
,  ,
, 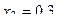 ,
,  . Вычислим соответствующие значения искомой функции:
. Вычислим соответствующие значения искомой функции:




Результаты вычислений представим в таблице.
Ответ:

| 0 | 0.1 | 0.2 | 0.3 | 0.4 |
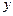
| 1 | 1.1 | 1.22 | 1.362 | 1.5282 |
|
из
5.00
|
Обсуждение в статье: Примеры решения типовых задач |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

