 |
Главная |
ОБЩЕЕ УТВЕРЖДЕНИЕ, частным случаем которого является Великая теорема Ферма 7 страница
|
из
5.00
|
Часть 2
Случаи (либо b = ± 1, либо c = ± 1) ОТСУТСТВУЮТ.
**********
Часть первая (Утверждения 2)
Уравнение 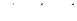 (
(  - четное, q = 4 = 2 m , где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах
- четное, q = 4 = 2 m , где m = 2) не имеет решений в отличных от нуля попарно взаимно простых целых числах  ,
,  и
и  таких, чтобы
таких, чтобы  - было четным,
- было четным,  и
и  - нечетными целыми числами.
- нечетными целыми числами.
Доказательство
Итак, имеем уравнение 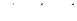 (1), где
(1), где  - четное, числаa, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 2»), среди которых только одно четное число a.
- четное, числаa, b, c (если, конечно, они существуют) – попарно взаимно простые целые числа (это наше допущение – вопреки «Утверждению 2»), среди которых только одно четное число a.
Из уравнения (1) следует: 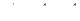 =>
=>  (2).
(2).
Пусть  (3), где
(3), где  и β - целые числа, отличные от нуля и c 2 + b 2 = 2 β (4), где β – нечетное число при c и b - нечетных.
и β - целые числа, отличные от нуля и c 2 + b 2 = 2 β (4), где β – нечетное число при c и b - нечетных.
*********
Примечание
То, что β в уравнении (4) нечетное число, хорошо известный факт в теории чисел, который легко доказывается.
Представим нечетные числа b и c в виде:
b = 2 n 1 + 1; c = 2 n 2 + 1,
где n 1 и n 2- произвольные целые числа. Тогда
b 2 + c 2 = (2 n 1 + 1)2 + (2 n 2 + 1)2 = 2 [2 (n12+n22+n1+n2) + 1],
где в квадратных скобках нечетное число, что и требовалось доказать.
*******
Тогда из уравнения (2) следует (с учетом (3) и (4):
 =
=  , где c 2 + b 2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
, где c 2 + b 2 ≠ 0, т.к. c ≠ 0, b ≠ 0, т.е.
 (5),
(5),
где k – целое число, отличное от нуля, т.к. c и b взаимно простые целые числа (при  – целое число k - четное число , т.к.
– целое число k - четное число , т.к.  пропорционально 4 (явно) при b и с – нечетных числа => 2l-2k – четное число при
пропорционально 4 (явно) при b и с – нечетных числа => 2l-2k – четное число при  ).
).
Из соотношений (4) и (5) определяем b 2 и c 2:
 =>
=>  =>
=> 
Откуда β = b 2 + 2 l -2 k (8) - нечетное число (из (4)) при b – нечетном и 2l-2k - четном.
*********
Вывод:
1. Из соотношения (4) имеем:
(9)  - нечетное число.
- нечетное число.
2. Из соотношения (5) имеем:
(10)  пропорционально 2 (явно), т.е.
пропорционально 2 (явно), т.е.  - четное число.
- четное число.
Это дополнительная информация о свойствах предполагаемых взаимно простых числах  , которая в дальнейшем нам очень пригодится.
, которая в дальнейшем нам очень пригодится.
*******
Теперь попробуем выразить сумму четвертых степеней чисел c и  . Учитывая соотношения (6) и (7), получим:
. Учитывая соотношения (6) и (7), получим:
 ,
,

 т.е.
т.е. 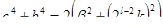 (11),
(11),
где  - целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для
- целые числа, которые, в свою очередь, как мы знаем из предыдущего доказательства «Утверждения 1» (для  ), могут быть выражены через другие целые числа
), могут быть выражены через другие целые числа  следующим образом:
следующим образом:
(12)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(13)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(14)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(15)  - четное число.
- четное число.
Примечание: во всех последующих исследованиях (Случаях) нас не будут интересовать t =0 и r =0 (при t =0  и
и 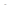 - четные из (12) и (13), при r =0
- четные из (12) и (13), при r =0  = 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению). .
= 0 (из (15)) => а = 0 (из (3)), что противоречит нашему допущению). .
*******
Для простоты опять обозначим правые части уравнений (12), …, (15) буквами С, В, N, К, т.е.
 = С
= С
 = В
= В
 = N
= N
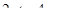 = К,
= К,
и рассмотрим случай, когда в правых частях уравнений (12), …, (15) перед С, В, N, К, стоят «плюсы» и выполняется Условие1.
********
Условие1 (начало)
с2 = С
b 2 = B
 = N
= N

Случай «+».
(12+)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(13+)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(14+)  - нечетное число при
- нечетное число при  - нечетном;
- нечетном;
(15+)  - четное число.
- четное число.
Казалось бы, все нормально: четность чисел  в (12+),…, (15+) совпадают при
в (12+),…, (15+) совпадают при  - нечетном с нашими предыдущими рассуждениями.
- нечетном с нашими предыдущими рассуждениями.
Однако не все так просто.
Помимо всего прочего, у нас есть еще две дополнительные информации (9) и (10) (о четности, заключенной в «Выводе» (стр.36)), вытекающие из предположения о том, что, вопреки условию «Утверждения 2», допустим, существуют попарно взаимно простые целые числа  .
.
Попробуем найти сумму  , воспользовавшись их выражениями (12+) и (13+):
, воспользовавшись их выражениями (12+) и (13+):
 ,
,
т.е.  => (
=> (  ) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
) пропорционально 4, откуда следует, учитывая (9) в «Выводе» (стр.36),
 !
!
Т.е., вопреки «Выводу»,  является не нечетным, а четным числом, что возможно (из (14)) при
является не нечетным, а четным числом, что возможно (из (14)) при  - четном.
- четном.
Однако, если  - четное, то
- четное, то  (в (12+) и (13+)) являются четными, т.е. в уравнениях (2)
(в (12+) и (13+)) являются четными, т.е. в уравнениях (2) 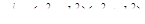 и (1)
и (1) 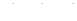 числа
числа  - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию в Случае «+» с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
********
Вывод. Следовательно, это уравнение (1) 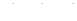 в данном Условии 1 (начало) не имеет решений в целых попарно взаимно простых
в данном Условии 1 (начало) не имеет решений в целых попарно взаимно простых  отличных от нуля числах, где
отличных от нуля числах, где  - четное натуральное число.
- четное натуральное число.
********
Мы рассмотрели случай, когда перед скобками в (12+), …, (15+) стояли «плюсы».
Случай, когда перед теми же скобками стоят «минусы» (Случай «-»), аналогичен вышерассмотренному. Вывод тот же. (СмотриСлучай «-» на стр.8.)
********
Примечание
Осталось рассмотреть еще 14 случаев, когда перед С, В, N, К стоятвсевозможные знаки (плюсы и минусы). Но об этом - во 2-ой части данного Утверждения 2.
********
Т.к. уравнение (11) симметрично для с2 и b2, (для уравнения (11) они равнозначны), то с2 и b 2 могут меняться своими выражениями ( C и В). Это свойство назовем «новым свойством  ». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять перед теми же В, С, N и К стоят одинаковые знаки.
». Поэтому аналогичны вышерассмотренному и случаи («Новые» случаи «+» и «-»), когда опять перед теми же В, С, N и К стоят одинаковые знаки.
Условие 2 (начало)
с2 = В
b 2 = С
 = N
= N

«Новые» случаи «+» и «-».
(12´±) c 2  =± В
=± В
(13´±) b2  =±С
=±С
(14±)  =±N
=±N
(15±)  =±К.
=±К.
И в этом случае сумма  пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)),
пропорциональна 4, откуда следует, (учитывая (13) в «Выводе» (стр.36)),  !
!
Т.е., вопреки «Выводу», и в этих «Новых» случаях «+» и «-»  является не нечетным, а четным числом, что возможно(из (14±)) при
является не нечетным, а четным числом, что возможно(из (14±)) при  -четном.
-четном.
Однако, если  - четное, то
- четное, то  (в ((12´±) и ((13´±)) являются четными, т.е. в уравнениях (2) и (1) числа
(в ((12´±) и ((13´±)) являются четными, т.е. в уравнениях (2) и (1) числа  - четные, а потому не являются попарно взаимно простыми целыми числами.
- четные, а потому не являются попарно взаимно простыми целыми числами.
Мы пришли к противоречию (в «Новых» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
*******
Вывод . Следовательно, это уравнение (1) в данном Условии 2 (начало) не имеет решений в целых попарно взаимно простых  отличных от нуля числах.
отличных от нуля числах.
*******
Примечание
Осталось рассмотреть еще 14 случаев,рассматривающих «новые свойства  », когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
», когда перед С, В, N, К стоят всевозможные знаки (плюсы и минусы).
Но об этом - во 2-ой части данного Утверждения 2.
********
Уравнение (11  ) симметрично и для
) симметрично и для  и для
и для  (для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями ( N и К). Это свойство назовем «похожим свойством
(для уравнения (11) они равнозначны), которые тоже могут меняться своими выражениями ( N и К). Это свойство назовем «похожим свойством  и
и  ». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых
». А это означает, что нам придется рассмотреть еще 16 «похожих» случаев (с 1-го по 14 и случаи «+» и «-», в которых  и
и  меняются своими выражениями ( N и К)).
меняются своими выражениями ( N и К)).
Условие 3 .
с2 = С
b 2 = B
 = К
= К

« Похожие» случаи «+» и «-».
(12±) c 2 = ± (  ) = ± С
) = ± С
(13±) b2 = ± (  ) = ± В
) = ± В
(14´±)  =
=  = ±К
= ±К
(15´±) 
 = ± N
= ± N
Согласно одному из Выводов (формула (10)  пропорционально 2 (явно), при
пропорционально 2 (явно), при  . Но это возможно, глядя на четное (15´±)
. Но это возможно, глядя на четное (15´±)  = ±N= ±(
= ±N= ±(  ) только при t- четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
) только при t- четном, при которых в (12±) и (13±) c и b – четные, чего не должно быть.
Мы пришли к противоречию (в «Похожих» случаях «+» и «-») с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
*******
В остальных 14 «похожих» случаях, где опять же  = ± N= ± (
= ± N= ± (  ) и перед С, В, N, К стоятвсевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства
) и перед С, В, N, К стоятвсевозможные знаки (плюсы и минусы), рассуждая аналогичным способом (и при этом не затрагивая «новые свойства  » (пояснение (стр.10), подобное для
» (пояснение (стр.10), подобное для  при доказательстве Утверждения 1), мы придем к прежнему результату: c и b – четные, чего не должно быть.
при доказательстве Утверждения 1), мы придем к прежнему результату: c и b – четные, чего не должно быть.
Это значит, что мы опять придем к противоречию с нашим предположением о существовании у уравнения (1) попарно взаимно простых целых  решений.
решений.
********
Вывод. Следовательно, это уравнение (1) в данном Условии 3 не имеет решений в целых попарно взаимно простых  отличных от нуля числах.
отличных от нуля числах.
*******
Вывод
1. Таким образом, в вышеприведенных Условиях 1 (начало), 2 (начало) и 3 уравнение (1)  (1), где
(1), где  - четное натуральное число, не имеет решений в целых попарно взаимно простых
- четное натуральное число, не имеет решений в целых попарно взаимно простых  отличных от нуля числах.
отличных от нуля числах.
2. 1-я часть «Утверждения 2» (для Условий 1(начало), 2 (начало) и 3) доказана.
*********
Часть вторая (Утверждения 2)
Случаи (либо b = ± 1, либо c = ± 1) ОТСУТСТВУЮТ.
Доказательство
Казалось бы, мы должны рассмотреть еще моменты в Условиях 1 и 2, когда перед скобками в (12), …, (15) стоят разные знаки (как при доказательстве «Утверждения 1» в части 2). Интуиция подсказывает, что эта процедура опять нас приведет к известным значениям b и c: либо  (из
(из  ), либо
), либо  (из
(из  ), либо b и c - четные чего не должно быть, (подобно доказательству части 2 «Утверждения 1»).
), либо b и c - четные чего не должно быть, (подобно доказательству части 2 «Утверждения 1»).
Для подтверждения сказанного рассмотрим подробно только часть Условия 1.
Условие 1 (продолжение).
Случай 1.
 (12)
(12)
 (13′)
(13′)
 (14)
(14)
 (15) ,
(15) ,
которые также являются решениями уравнения (11)
 .
.
Тогда сумма  имеет вид:
имеет вид:

Учитывая (10) и (15), можно получить разность  :
:


 =>
=>  .
.
|
из
5.00
|
Обсуждение в статье: ОБЩЕЕ УТВЕРЖДЕНИЕ, частным случаем которого является Великая теорема Ферма 7 страница |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

