 |
Главная |
Рассуждение старшеклассника
|
из
5.00
|
Рассмотрю два числа: 43714 и 74314. Представлю эти числа как сумму трех слагаемых при помощи позиционной записи числа: 43714=4.142+3.14+7 74314=7.142+4.14+3. Замечу, что любое трехзначное число в 14-ной системе счисления можно записать в виде: a2a1a0 14 =a2. 142+a1.14+a0. Мне известно свойство делимости суммы: Если каждое слагаемое суммы делится на 7, то сумма делится на 7. Из того, что 14 делится на 7, следует, что сумма первых двух слагаемых всегда будет делиться на 7. Для того, чтобы вся сумма делилась на 7 необходимо, чтобы последнее слагаемое этой суммы делилось на 7. А последнее слагаемое в сумме a2. 142+a1.14+a0 - это последняя цифра в записи числа a2a1a0 14. Использовали Свойство делимости суммы: Дано G+C+D/ G  K; C
K; C  K; D
K; D  K
K 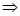
(G+C+D)  K
K
Определение отношения делимости


|
Вывод: Число a2a1a0 14 в 14-ной системе счисления кратно 7, если последняя цифра в его записи 7 или 0.
Тогда 43714 -кратно, а 74314 -не кратно.
Утверждение 1.
Любое трехзначное число в 14-ичной системе счисления делится на 7 в том и только в том случае, когда последняя цифра этого числа делится на 7.
Замечание 1. Если для делимости необходимо, чтобы последняя цифра (разряд единиц) делилась на 7, то не важно, сколько разрядов будет иметь число. Их может быть n.
Замечание 2. Число an. 14n+…+a1.14+a0
делится на 7, т.к. 14 делится на 7. Если в утверждении 1 вместо 14 взять основание 7 или 28, или другие числа, делящиеся на 7, то получится также справедливое утверждение:
Утверждение 2.
Пусть число А записано в системе счисления, основание которой делится на 7. Тогда число А делится на 7 в том и только в том случае, когда его последняя цифра делится на 7.
Результат моего исследования можно представить в виде теоремы.
Теорема: 

Доказательство.

Последняя сумма делится на 7 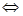 р
р  7,а0
7,а0  7. Теорема доказана.
7. Теорема доказана.
Приложение 2
Тексты описывающие “ход исследования”, опробованные в Школе молодого ученого.
Признак делимости на 7
Задача1. Вывести признак делимости на 7.
Так как задача общая, уточним систему счисления, в которой будем решать задачу. Например, возьмем системы счисления по основанию 7 и 14.
Задача 2. Вывести признак делимости на 7 в 7-ной и 14-ной системах счисления.
Задачу решали три ученика: младший школьник, ваш ровесник и старшеклассник.
Рассуждение 1
Выпишу все двузначные числа в 7-ной системе счисления. Это числа:107, 117, 127, 137, 147, 157, 167, 207, 217, 227, 237, 247, 257, 267, 307, 317, 327, 337, 347, 357, 367, 407, 417, 427, 437, 447, 457, 467, 507, 517, 527, 537, 547, 557, 567, 607, 617, 627, 637, 647, 657, 667.
Возьму и выпишу из них все двузначные числа, делящиеся на 7. Это числа:107, 207, 307, 407, 507, 607.
Вижу, что на 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.
Так же возьму и выпишу все однозначные и двузначные числа в 14-ной системе счисления делящиеся на 7.
14, 1014, 1714, 2014, 2714, 3014, 3714, 4014, 4714, 5014, 5714, 6014, 6714, 7014, 7714, 8014, 8714, 9014, 9714.
Вижу, что на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.
Я перебрал все числа, поэтому делаю вывод, что:
) На 7 в 7-ной системе счисления делятся двузначные числа, оканчивающиеся на 0.
) на 7 в 14-ной системе счисления делятся двузначные числа, оканчивающиеся на 0 и 7.
Рассуждение 2
Требуется найти признак делимости на 7 в 7-ичной и 14-ной системе счисления. Может мне удастся подметить закономерность в записи чисел делящихся на 7 в 7-ной и 14-ной системах счисления.
Выберу произвольно несколько чисел из этих систем счисления. Например, числа: 3657; 2507; 1607; 5207; 43714; 79314; 34014; 34714; 87414. Переведя числа в десятичную систему счисления и поделив на 7, я обнаружил, что на 7 делятся следующие числа:
7; 1607; 5207; 43714; 34014; 34714.
Как увидеть закономерность? На что смотреть? В случае признака делимости на 9 в десятичной системе счисления смотрели, например, на сумму цифр числа. Посмотрю и здесь.
7 2+5+0=7:7
7 1+6+0=7:7
7 5+2+0=7:7
14 4+3+7=14:7
14 3+4+0=7:7
14 3+4+7=14:7
Вижу, что сумма цифр числа всегда делится на 7.
Мне кажется верным предположение: на 7 в 7-ной и 14-ной системах счисления делятся те числа, сумма цифр, в записи которых делится на 7. Для чисел 2507; 1607; 5207; 43714; 34014; 34714 мое предположение верно. Но верно ли оно для любого числа?
| Переставлю цифры в числе 43714 (от этого сумма цифр не изменится) и получу число 74314.. Сумма цифр этого числа делится на 7, но само число не делится на 7. Это можно проверить переводом числа из 14-ной системы счисления в 10-ную и делением на 7. | Контрпример- это пример, опровергающий утверждение. |
Следовательно, мое предположение для любого числа неверно и нужно искать другую закономерность.
Еще в случае признаков делимости на 2 и 5 в 10-ной системе счисления смотрели на последнюю цифру числа. Посмотрю и здесь. Вижу, что на 7 в 7-ной и 14-ной системах счисления делятся числа оканчивающиеся на 0 или 7.
Сделаю предположение: на 7 в 7-ной и 14-ной системах счисления делятся числа, оканчивающиеся на 0 или 7.
Предположение опровергнуть мне не удалось, поэтому я думаю, что оно верно для любых чисел в 7-ной и 14-ной системах счисления.
Рассуждение 3
Мне известно свойство делимости суммы: если каждое слагаемое суммы делится на 7, то сумма делится на 7. Попробую применить это свойство для вывода признака делимости на 7.
Рассмотрю два числа: 43714 и 74314. Представлю эти числа как сумму трех слагаемых при помощи позиционной записи числа:
43714=4.142+3.14+7
14=7.142+4.14+3.
Замечу, что любое трехзначное число a2a1a0 14 в 14-ной системе счисления можно записать в виде суммы трех слагаемых
a2a1a0 14 =a2. 142+a1.14+a0
Из того, что 14 делится на 7, следует, что a2. 142+a1.14 всегда будет делиться на 7. Для того, чтобы вся сумма делилась на 7 нужно, чтобы последнее слагаемое этой суммы также делилось на 7. А последнее слагаемое в сумме a2. 142+a1.14+a0 - это последняя цифра в записи числа a2a1a0 14.
Можно сделать вывод, что число a2a1a0 14 в 14-ной системе счисления кратно 7, если последняя цифра в его записи 7 или 0.
Видно, что 43714 -кратно, а 74314 -не кратно семи.
Теперь я могу сформулировать верное утверждение:
Утверждение 1.Любое трехзначное число в 14-ичной системе счисления делится на 7 в том и только в том случае, когда последняя цифра этого числа делится на 7.
Просматривая еще раз свое решение, я заметил две вещи:
) если для делимости необходимо, чтобы последняя цифра (разряд единиц) делилась на 7, то не важно, сколько разрядов будет иметь число. Их может быть n;.
2) число an…a0 14 =an. 14n+…+a1.14+a0 делится на 7, т.к. 14 делится на 7. Вместо 14 взять числа 7 или 28, или другие числа, делящиеся на 7, и мой признак делимости остается справедливым.
Теперь я могу сформулировать верное утверждение:
Утверждение 2.
Пусть число А записано в системе счисления, основание которой делится на 7. Тогда число А делится на 7 в том и только в том случае, когда его последняя цифра делится на 7.
Я могу представить результат своего исследования в виде теоремы.
Теорема: Число 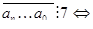

Доказательство. Верны равенства

Из свойства делимости суммы следует, что последняя сумма делится на 7 тогда и только тогда, когда р Знак 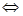 делится на 7 и
делится на 7 и  делится на 7.Теорема доказана.
делится на 7.Теорема доказана.
Приложение 3
Карточки с заданиями для занятия 2 в Школе молодого ученого. Определить, истинны ли утверждения:
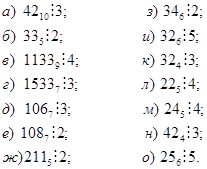
Приложение 4
Итоговый вариант текстов описывающих “ход исследования”.
|
из
5.00
|
Обсуждение в статье: Рассуждение старшеклассника |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

