 |
Главная |
Уравнения метода конечных элементов: теория упругости.
|
из
5.00
|
Наша конечная цель — получить для узловых величин такие числовые значения, при которых соотношения для элементов очень точно аппроксимируют некоторый важный физический параметр. В задачах теории поля (перенос тепла, течение грунтовых вод, расчет магнитных полей и др.) минимизировался некоторый функционал. Этот функционал обладает тем свойством, что любая минимизирующая его функция удовлетворяет как исходным дифференциальным уравнениям, так и граничным условиям. Окончательные результаты, как для задач теории поля, так и для задач теории упругости, представлены в виде поверхностных и объемных интегралов, которые вычисляются при рассмотрении конкретных областей применения. [14]
Решение задач теории упругости может быть проведено одним из двух методов. С помощью первого метода решают дифференциальные уравнения с заданными граничными условиями. Второй метод заключается в минимизации интегральной величины. Для решения задач теории упругости методом конечных элементов используется последний подход. Если задача решается в перемещениях и на границе заданы их значения, то нужно минимизировать потенциальную энергию системы. Если задача решается в напряжениях с заданными на границе усилиями, то нужно минимизировать дополнительную работу системы. Общепринятая формулировка метода конечных элементов предполагает отыскание поля перемещений и тем самым связана сминимизацией потенциальной энергии системы при отыскании, узловых значений вектора перемещений. После того как перемещения будут определены, можно вычислить компоненты тензоров деформаций и напряжений. [14], [15]
Поскольку далее мы будем пользоваться формулировкой метода конечных элементов, связанной с минимизацией потенциальной энергии, приведем здесь теорему о потенциальной энергии.
Из всех перемещений, удовлетворяющих кинематическим гра ничным условиям, стационарное (экстремальное) значение потенциальной анергии сообщают те перемещения, которые удовлетворяют уравнениям, равновесия.
Важное требование этой теоремы состоит в том, что искомые перемещения должны удовлетворять заданным значениям на границе.
Полная потенциальная энергия упругой системы может быть разделена на две части, одна из которых соответствует энергия деформаций в теле, а другая определяется потенциальной энергией массовых сил и приложенных поверхностных сил. В соответствии с этим запишем полную потенциальную энергию в виде
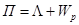 , (3.7)
, (3.7)
где 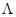 —энергия деформаций, a —потенциальная энергия приложенных сил. Работа внешних сил противоположна по знаку их потенциальной энергии:
—энергия деформаций, a —потенциальная энергия приложенных сил. Работа внешних сил противоположна по знаку их потенциальной энергии:
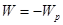 . (3.8)
. (3.8)
Из формул (3.7) и (3.8) получаем
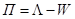 . (3.9)
. (3.9)
После разбиения области на элементы равенство (3.9) записывается е виде суммы
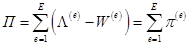 . (3.10)
. (3.10)
Общий случай.
Энергия деформации бесконечно малого объема dV дается формулой
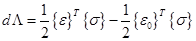 , (3.11)
, (3.11)
где 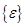 —полная деформация, а
—полная деформация, а 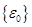 —начальная деформация. Величина
—начальная деформация. Величина 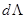 называется плотностью энергии деформации, аполная энергия деформации получается интегрированием этой величины по объему тела:
называется плотностью энергии деформации, аполная энергия деформации получается интегрированием этой величины по объему тела:
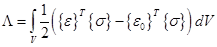 . (3.12)
. (3.12)
Вид векторных столбцов 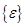 и
и 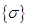 зависит от того, какая задача решается. Например, для двумерного случая плоской деформации эти вектор - столбцы имеют вид
зависит от того, какая задача решается. Например, для двумерного случая плоской деформации эти вектор - столбцы имеют вид
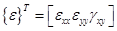
и
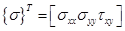 .
.
В основе курса теории упругости лежат два важных соотношения: закон Гука, который связывает компоненты тензоров напряжений и деформаций, и соотношения связи между деформациями и перемещениями. Закон Гука в общей форме имеет вид
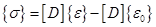 , (3.13)
, (3.13)
где [ D ] содержит упругие константы материала. Соотношения связи между деформациями и перемещениями записываются как
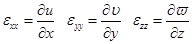 ,
,
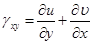 ,
, 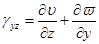 ,
, 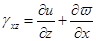 , (3.14)
, (3.14)
где и, 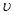 и w — компоненты перемещений в направления координатных осей х, у и z соответственно[2]. Эти компоненты перемещений были выражены в гл. 3 через узловые значения следующим образом:
и w — компоненты перемещений в направления координатных осей х, у и z соответственно[2]. Эти компоненты перемещений были выражены в гл. 3 через узловые значения следующим образом:
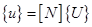 . (3.15)
. (3.15)
Здесь [ N ] —матрица функций формы. С помощью формул (3.14) можно выразить вектор деформации 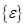 через узловые перемещения { U }.Общая форма этих соотношений такова
через узловые перемещения { U }.Общая форма этих соотношений такова
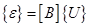 . (3.16)
. (3.16)
Здесь [В] —матрица, получаемая дифференцировал нем надлежащим образом матрицы [ N ]. Фактические значения коэффициентов матрицы [В] зависят от вида используемого элемента и от типа рассматриваемой задачи. Поэтому точное определение [В] будет отложено до рассмотрения конкретных примеров. [30]
Энергия деформации 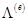 отдельного элемента с помощью формул (3.13) и (3.16) может быть записала в следующем виде:
отдельного элемента с помощью формул (3.13) и (3.16) может быть записала в следующем виде:
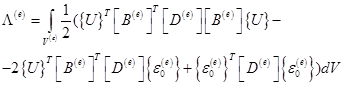 . (3.17)
. (3.17)
Последнее слагаемое в (5.68) не зависит от узловых значений 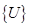 , поэтому оно не влияет на процесс минимизации и в дальнейших ссылках не будет приниматься во внимание. [30]
, поэтому оно не влияет на процесс минимизации и в дальнейших ссылках не будет приниматься во внимание. [30]
Работа, совершаемая внешними силами, может быть разделена на три различные части: работа 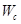 , совершаемая сосредоточенными силами, работа
, совершаемая сосредоточенными силами, работа 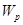 , которая получается в результате действия компонент напряжений на внешней стороне поверхности, работа
, которая получается в результате действия компонент напряжений на внешней стороне поверхности, работа 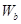 , совершаемая массовыми силами.
, совершаемая массовыми силами.
Работу сосредоточенных сил легко определить, если в каждой точке приложения сосредоточенной силы поместить узел. Работа сосредоточенной силы равна произведению величины этой силы на длину пути, нa котором эта сила действует. Таким образом, работа отдельной силы равна 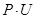 . Обозначая узловые силы через {Р}, а узловые перемещения через { U }, совершенную работу можно записать в виде произведения матриц:
. Обозначая узловые силы через {Р}, а узловые перемещения через { U }, совершенную работу можно записать в виде произведения матриц:
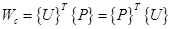 . (3.18)
. (3.18)
Это определение предполагает, что силы разложены на компоненты, параллельные компонентам перемещений. Эта часть полной работы не входит в сумму (3.2), так как рассмотренные силы сосредоточены в узлах. [30], [34]
Работа объемных сил χ, ỳ, £дается формулой
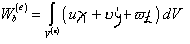
где и, 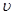 и w — компоненты вектора перемещений внутри элемента по осям х, у и z соответственно. Интеграл здесь необходим, так как и,
и w — компоненты вектора перемещений внутри элемента по осям х, у и z соответственно. Интеграл здесь необходим, так как и, 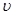 и
и 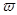 вместе с χ, ỳ и £могут изменяться внутри элемента. Используя равенство (3.14), формулу (3.18) можно переписать в виде
вместе с χ, ỳ и £могут изменяться внутри элемента. Используя равенство (3.14), формулу (3.18) можно переписать в виде
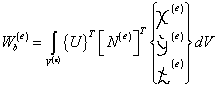 . (3.19)
. (3.19)
Работа поверхностных сил определяется следующим образом:
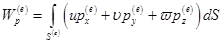 , (3.20)
, (3.20)
где и, 
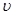 и w — компоненты вектора перемещений, а рх, py и pz — компоненты вектора напряжений, параллельные координатным осям х, у и z .
и w — компоненты вектора перемещений, а рх, py и pz — компоненты вектора напряжений, параллельные координатным осям х, у и z .
Сравнение формул (3.20) и (3.18) показывает, что они идентичны по форме. Поэтому
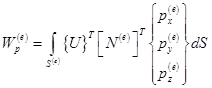 . (3.21)
. (3.21)
Используя формулы (3.2), (3.10), (3.17), (3.19) и (3.21), получаем выражение для полной потенциальной энергии:
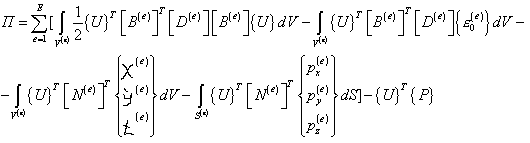 , (3.22)
, (3.22)
Чтобы минимизировать величину П, продифференцируем выражение (3.22) по { U } в приравняем результат нулю. Эту операцию можно выполнить, используя дифференциальные соотношения Б1 и Б2. В результате будем иметь
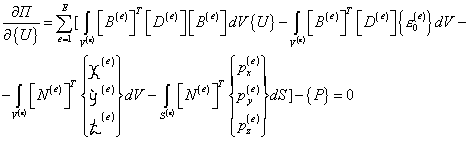 . (3.23)
. (3.23)
Интегралы в формуле (3.23) определяют для каждого элемента вектор нагрузки { f ( e ) } и матрицу жесткости 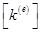 , которые можно объединить следующим образом:
, которые можно объединить следующим образом:
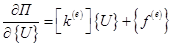 . (3.24)
. (3.24)
В рассматриваемом случае 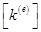 — объемный интеграл вида
— объемный интеграл вида
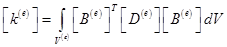 , (3.25)
, (3.25)
а 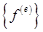 —сумма нескольких интегралов:
—сумма нескольких интегралов:
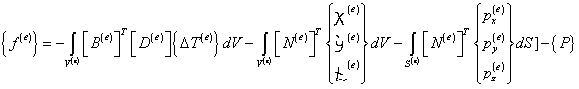 (3.26)
(3.26)
Матрица жесткости элемента (3.25) не содержит поверхностный интеграл, который встречается в задачах теории поля. [30]
Глобальная матрица жесткости [К] и глобальный вектор-столбец { F } вматричном уравнении
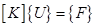 (3.27)
(3.27)
даются соотношениями
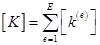 , (3.28)
, (3.28)
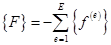 . (3.29)
. (3.29)
|
из
5.00
|
Обсуждение в статье: Уравнения метода конечных элементов: теория упругости. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

