Вариационный принцип Лагранжа.

Теоретическая основа МКЭ базируется на известном принципе возможных перемещений Лагранжа, который формулируется так: «если система материальных точек находится в равновесии, то работа всех приложенных к ней сил на любых возможных бесконечно малых отклонений от положения равновесия равна нулю». [16]

Использовать принцип Лагранжа целесообразно потому, что в задаче динамики присутствуют силы инерции, которые определяются через перемещения.

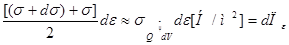
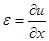(безразмерная величина)

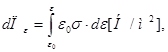
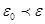     (3.2.1)

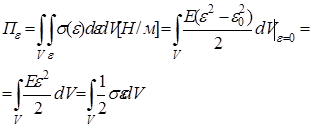3.2.2)

Рис.6

В трехмерном случае:

 

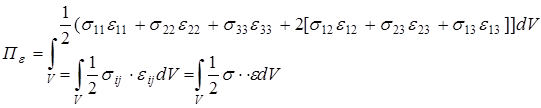
Элементарная работа внутренних сил:

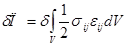
В последней формуле символ «d» обозначает кинематически допустимую вариацию, т.е. произвольно изменяется поле перемещений на бесконечно малую величину d`u, причем кинематчески краевые условия (ограничения на перемещение некоторых точек тела) остаются справедливыми как для вектора перемещений `u, так и для его вариации.

При малых деформациях объем, по которому производится интегрирование, можно считать неизменным, и поменять местами символы интегрирования и варьирования.

Если выполняется обобщенный закон Гука, то подынтегральное выражение есть квадратичная форма по компонентам деформации:

s_ij e_ij = C_kmij e_km e_ij, тогда

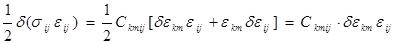(3.2.3)

Работа внутренних сил:

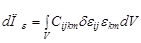                                 (3.2.4)

Элементарную работу внутренних сил для упругого тела отождествляют с потенциальной энергией деформируемого состояния. [11]

Если к телу приложены внешние массовые, поверхностные и сосредоточенные силы, то они совершают работу на перемещениях точек, лежащих внутри тела и на его границах.

Если задана кинематически допустимая вариация d`u, то элементарная работа внешних сил вычисляется по формуле:

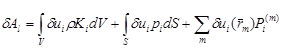              (3.2.5)

Векторы `r<sub>m</sub> есть радиус-векторы точек приложения сосредоточенных сил `P_m.

Если пренебречь эффектами выделения тепла при деформировании и считать процесс деформации адиабатическим, то элементарные работы внешних и внутренних сил равны между собой. Тогда вариационное уравнение принимает вид:

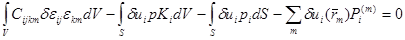              (3.2.6)

Представленная общая форма принципа возможных перемещений может быть модифицирована путем принятия некоторых кинематических и статических гипотез. В частности для стержней гипотеза Бернулли приводит к тому, что из всех слагаемых, определяющих потенциальную энергию деформаций ненулевым становится только одно, определяющее деформацию растяжения/сжатия волокон, параллельных оси стержня. [3]

В связи с тем, что принятие этой гипотезы приводит к линейному распределению перемещений по площади поперечного сечения, а также к линейному распределению деформаций, то можно вычислить интегралы по площади поперечного сечения.

Тогда вариационное уравнение будет содержать только интеграл по длине стержня

                      

 

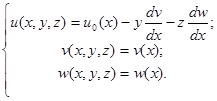
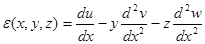
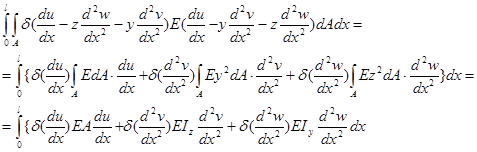
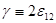
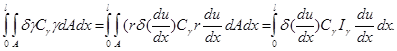    (3.2.7)

Все слагаемые с поперечными координатами в первой степени и их произведениями уничтожаются при интегрировании, т.к. выбранная система координат есть главная центральная система поперечного сечения. [11]

В теории стержней помимо сосредоточенных сил рассматриваются сосредоточенные моменты. Дополним выражением вариационного принципа возможной работой сосредоточенных моментов М_x, М_y, М_z [Н-м]

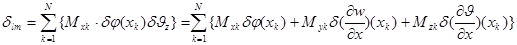
Окончательно принцип возможных перемещений для стержня следует записать в виде:

               (3.2.8)

Рис.7

В последней формуле p_x, p_y, p_z – компоненты нагрузки, распределенной вдоль оси стержня; m_x, m_y, m_z – компоненты момента, распределенного вдоль оси стержня, х_k – точка приложения сосредоточенных сил и моментов Р_хk, Р_уk, … М_zk.

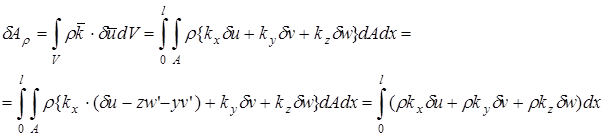
Данная формула справедлива только в том случае, если компоненты массовой силы k_x, k_y, k_z равномерно распределены по поперечному сечению с координатой х, а также при постоянной по сечению плотности.

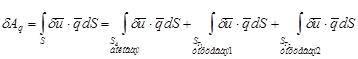                  (3.2.9)

Последние два интеграла представляют собой работу сосредоточенной силы и сосредоточенного момента, которые являются главным вектором и главным моментом распределенной по торцу нагрузки q. [30]

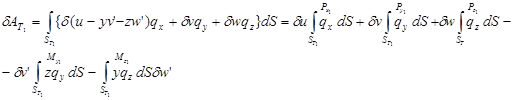(3.2.10)

,

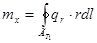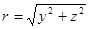
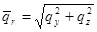
Приведенные рассуждения показывают, что распределенные по торцам нагрузки действительно можно заменить их главными векторами и главными моментами относительно центра тяжести поперечного сечения.

Проделаем аналогичное рассуждение для произвольного поперечного сечения с текущей координатой х и рассмотрим работу нагрузок, распределенных по боковой поверхности стержня.

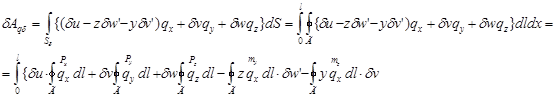
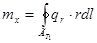                                                        (3.2.11)

q_t = `q×`n(r)

Распределенными изгибающими и крутящими моментами для тонких стержней обычно пренебрегают в силу малости этих величин, имеющих порядок m_x, m_y, m_z ~ 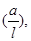 где а – характерный поперечный размер стержня.

В дальнейшем при построении варианта метода конечных элементов для расчета стержней и стержневых систем будем использовать формулировку вариационного принципа (3.2.8), пренебрегая распределенными моментами m_x, m_y, m_z.

Будем рассматривать вариант метода конечных элементов в перемещениях на основании вариационного уравнения Лагранжа. Будем считать, что конечно-элементная сетка задана, т.е. установлено соответствие между номерами узлов и номерами конечных элементов и определены координаты узлов. Для каждого конечного элемента будем считать заданными функции формы так, что перемещение произвольной точки, принадлежащей конечному элементу, однозначно определяется перемещениями его узлов

`u(`r) = [Ф(`r)]`q_n,        `r Î v_n                                                                     (3.2.12)

v_n – многогранник, определяющий конечный элемент. Введем в рассмотрение векторы напряжений и деформации

`s = {s₁₁ s₂₂ s₃₃ s₁₂ s₂₃ s₁₃}

`e = {e₁₁ e₂₂ e₃₃ e₁₂ e₂₃ e₁₃}                                                        (3.2.13)

так, что произведение этих двух векторов дает работу

dA(r) = d`e <sup>T</sup>`s (`r )

`r – радиус-вектор произвольной точки.