Функции формы для кругового стержня.

Выпишем систему уравнений состояния плоского кругового стержня:

( 5.14)

и упростим ее, учитывая особенности геометрии стержня и считая отсутствующими внешние нагрузки. Кроме того, будем считать, что стержень совершает свободные колебания по закону:

.

тогда после преобразований, получим:

( 5.15)

Последняя однородная система уравнений определяет формы колебаний. Перепишем ее в матричной форме, вводя вектор состояния:

( 5.16)

и зависящую от параметра матрицу системы ( 5.15):

( 5.17)

Для решения этого уравнения используем универсальную подстановку:

,

где р играет роль параметра. Для его определения имеем характеристическое уравнение

( 5.18)

Прежде всего отметим, что структура матриц А и В такова, что на главной диагонали матрицы А – W²В располагаются только нулевые элементы и, следовательно, соблюдается соотношение между корнями ( 5.19)следующее из теоремы Виета [47]:

.

( 5.19)

Здесь tr(A)=A₁₁+ A₂₂+…+ A_nn – след матрицы А.

Нулевых корней быть не должно, так как им соответствует постоянная компонента, что противоречит уравнению ( 5.17). Так как среди корней встречаются вещественные, мнимые, и комплексные, то на основании ( 5.19) можно утверждать, что вещественные и мнимые корни могут встречаться только парами, симметричными относительно мнимой и вещественной осей, т.е. для всякого вещественного корня х>0 существует парный корень –х; для всякого мнимого iy (y>0) – корень –iy. Каждой паре комплексно сопряженных корней  должна соответствовать пара . В этом случае условие ( 5.19) выполняется автоматически. Вследствие этого можно представить характеристический полином в виде произведения:

,

( 5.20)

где Р₄ – полином 4-й степени по р, не имеющий нулевых корней. Таким образом, можно утверждать, что существует минимальный полином матрицы А₀ – w²В:

.

( 5.21)

Но в [47] показано, что корни минимального и характеристического полиномов совпадают в совокупности, и характеристический полином отличается от минимального только кратностью корней. Следовательно, других корней, кроме отмеченных выше, быть не может.

    Это обстоятельство существенно облегчает поиск корней характеристического уравнения: достаточно исследовать первый квадрант комплексной плоскости, включая вещественную и мнимую полуоси. Но нельзя забывать, что среди отмеченных восьми корней четыре могут быть кратными; обнаружить их можно, деля характеристический полином на соответствующий каждому корню двучлен или трехчлен. Если остаток от деления равен нулю при значении параметра р, равного корню, то этот корень – кратный. Отсюда можно определить функциональный базис для построения общего решения однородного уравнения ( 5.17): он будет состоять из собственных векторов матрицы А - w²В, домноженных на собственные функции вида  и , причем последние будут соответствовать только четырем кратным корням.

    Особенностью полученного решения является то, что и собственные векторы, и собственные числа (корни характеристического уравнения) будут зависеть от частоты свободных колебаний w, которая заранее не известна. Обозначим  матрицу решения, которая имеет следующий вид:

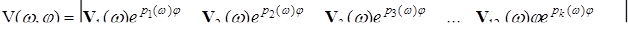
( 5.22)

причем последние четыре столбца – собственные векторы, соответствующие кратным корням и потребуем выполнения тождества:

и найдем произвольные постоянные С через условия в начале стержня:

;

Тогда общее решение, удовлетворяющее заданным начальным условиям, примет вид:

( 5.23)

Записывая ( 5.23) для конца стержня, получим:

( 5.24)

Но в число параметров вектора состояния входят шесть кинематических и шесть силовых параметров; выразим силовые параметры вектора Y(0) через кинематические параметры вектора Y_k. Для этого в последнем уравнении разобьем матрицу D и векторы на клетки:

,

где F – множество силовых параметров состояния, q – множество кинематических параметров. Из последнего уравнения имеем:

Из второго уравнения, записанного для произвольного угла j, получим:

( 5.25)

Из последнего уравнения видно, что матрица функций формы принимает вид:

( 5.26)

Таким образом, матрица функций формы построена на базисе строгих решений однородного уравнения, описывающего формы свободных колебаний кругового стержня.

    Исходя из структуры общего решения, в котором собственные векторы не зависят от j, можно утверждать, что во входящих в ( 5.26) матрицах у каждого столбца имеется скалярный множитель, зависящий от координаты j. Поэтому все операции дифференцирования и интегрирования, выполняемые над функциями формы при вычислении матричных характеристик КЭ (см. п. 5.2) могут быть выполнены над этими множителями.

 

ЗАКЛЮЧЕНИЕ

В работе рассмотрены вопросы конечноэлементного моделирования биомеханических систем. К таковым, в первую очередь, относится опорно-двигательный аппарат – скелет организма. Анализируя его состав, выяснено, что большая часть его элементов представляет собой криволинейные стержни. Таким образом, проблема моделирования биомеханических систем в кочестве основной включает задачу анализа состояний опорно-двигательного аппарата как системы криволинейных стержней.

Рассмотренные варианты метода конечных элементов позволяют сделать вывод о том, что массовым является применение полиномиальных функций формы. Один из вариантов таких функций – полиномы первой и третьей степени – были использованы в моей работе при решении задачи о свободных колебаниях витка цилиндрической пружины, который по своим геометрическим свойствам близок к элементам скелета. Результаты расчетов – частоты свободных колебаний – показали, что при небольшом ~10² количестве КЭ только первая частота получается близкой к аналитическому решению. Уточнение за счет измельчения сетки имеет ограниченные возможности, так как короткие КЭ имеют длину, сравнимую с размерами поперечного сечения и вряд ли их можно считать тонкими стержнями. Тогда перспективным становится направление, связанное с применением в качестве функций формы аналитических решений задач теории криволинейных стержней.

В работе предложен вариант построения конечного элемента в виде плоского стержня с круговой осью. В качестве функций формы использовались комбинации аналитических решений уравнений динамики кругового стержня. Решение тестовых задач показало, что спектр криволинейного стержня, полученный с помощью такого конечного элемента, дает хорошее приближение уже при количестве КЭ, на порядок меньшем, чем при использовании классических прямолинейных КЭ с полиномиальной аппроксимацией. Недостатком разработанного КЭ является необходимость решения сложного уравнения для определения частот свободных колебаний, причем в отличие от классической МКЭ-формулировки частотная задача не является задачей собственных значений линейной алгебры. Однако применение численного метода половинного деления, обладающего абсолютной сходимостью, позволяет решить эту задачу за обозримое время порядка 10..20 мин при использовании высокопроизводительных ПЭВМ.

 

ЛИТЕРАТУРА

1. Агапов В. П. Метод конечных элементов в статике, динамике и устойчивости пространственных тонкостенных подкрепленных конструкций. Учеб. пособие/М; Изд. АСВ, 200, 152 стр, с илл.

2. Биргер И. А. Стержни, пластинки, оболочки. – М.: Физматлит, 1992.- 392 с.-ISBN 5-02-014296-4.

3. Борискин О. Ф. Автоматизированные системы расчета колебаний МКЭ. – Иркутск: Изд-во Иркут. Ун-та, 1984. – 188 с.

4. Вальтер А. И., Дорохин Н. Б. Метод конечных элементов в технологических задачах пластичности: Учеб. пособие/ Тул. гос. ун-т. Тула. 1999. – 134 с.

5. Вибрации в технике./ Справочник в 6 томах // Т.3. Колебания машин, конструкций и их элементов. Под ред. Ф.М. Диментберга, К.С. Колесникова. – М.: Машиностроение, 1980. – 544с.

6. Вибрации в технике./ Справочник в 6 томах // Т.4. Вибрационные процессы и машины. Под ред. Э.Э. Лавендела. – М.: Машиностроение, 1981. – 510с.

7. Вибрации в технике: Справочник. В 6-ти т./Ред. В. Н. Челомей (пред). – М.: Машиностроение, 1980 – Т. З. Колебания машин, конструкций и их элементов/ Под ред. Ф. М. Диментберга и К.С. Колесникова. 1980. 544 с, ил.

8. Галлагер Р. Метод конечных элементов. Основы: Пер. с англ. – М.: Мир, 1984, - 428 с., ил.

9. Деклу Ж. Метод конечных элементов. Изд-во «Мир», Москва. 1986. Перевод на русский язык, «Мир», 1976.

10. Детали машин. Расчет и конструирование/ Справочник в 2-х томах Под ред. Н.С. Ачеркана.// Т.2. – М.: Машиностроение, 1968. _ 408с.

11. Диментберг Ф. М. Винтовое исчисление и его приложение в механике. Изд-во «Наука», гл.ред.физ-мат. лит-ры. М, 1965 г., 200 стр. и илл.

12. Донской Д. Д. Учеб.пособие для студентов фак. физ. воспитания пед. ин-тов. М., «Просвещение», 1975.

13. Ефимов Н. В. Краткий курс аналитической геометрии. М., 1975 г., 275 стр. с илл.

14. Желтков В. И. Лекции по курсу «Прикладные задачи механики твердого деформированного тела».

15. Зациорский В. М. и др. Биомеханика двигательного аппарата человека. Зациорский В.М., Аруин А. С., Селуянов В. Н. – М.: Физкультура и спорт, 1981. – 143 с. ил. – (Наука – спорту).

16. Зенкевич О., Морган К. Конечные элементы и аппроксимация: Пер. с англ. – М.: Мир, 1986.-318 с., ил.

17. Зенкевич О., Чанг И. Метод конечных элементов в теории сооружений и в механике сплошных сред. Нью-Йорк, 1967. Пер. с англ. А. П. Троицкого и С.В. Соловьева под ред. докт. техн. наук Ю. К. Зарецкого. М., «Недра».

18. Ильюшин А. А., Победря Б, Е. Основы математической теории термовязко-упругости. Изд-во «Наука». 1970.

19. Карнеев С. В., Карпухин В.П. Расчет оболочек с неканонической поверхностью методом конечных элементов и суперэлементов. – Тула: Тульский полиграфист, 2001. – 128 с.: ил.

20. Кац А. С. Расчет неупругих строительных конструкций. – Л.: Стройиздат, Ленинг. отд-ние, 1989. - 168 с., ил. ISBN 5-274-00367-2

21. Колокольцев В. А. Основы применения метода конечных элементов в расчетах деталей машин: учеб. пособие. Саратов: Сарат. гос. техн. ун-т, 2003. 84 с.

22. Корн Г., Корн Т. Справочник по математике.- М.: Мир, 1970. – 720с.

23. Красносельский М. А., Лифшиц Е.А., Соболев А. В. Позитивные линейные системы: метод положительных операторов. – М.: Наука. Главная редакция физико-математической литературы, 1985. – 256 с.

24. Крылов О. В. Метод конечных элементов и его применение в инженерных расчетах: учеб. пособие для вузов. – М.: Радио и связь, 2002. – 104 с.; ил.

25. Лурье А. И. Теория упругости. Изд-во «Наука», Гл. ред. физ-мат. Литературы. Москва, 1970 г.

26. Макушин В.М. Поперечные колебания и устойчивость пружин. / в кн. Динамика и прочность пружин. – М.: АН СССР, 1950 - 354с..

27. Механика твердых деформируемых тел. Техн. ред. Л. А. Белова. Производственно-издательский комбинат ВИНИТИ, Люберцы, Октябрьский пр., 403

28. Норри Д., де Фриз Ж. Введение в метод конечных элементов: пер. с англ. – М.: Мир, 1981. – 304 с., ил.

29. Победря Б. Е. Численные методы в теории упругости и пластичности. Изд-во Московского университета. 1981.

30. Пономарев С.Д. Расчет и конструкция витых пружин. – М.: ОНТИ, 1938 - 352с.

31. Работнов Ю.Н. Механика твердого деформируемого тела. Изд-во «Наука», гл. ред. физ.-мат. лит-ры. Москва. 1988.

32. Расчет изделий из высокоэластического материала / С.И. Дымников, Э.Э. лавендел, А.А. Павловский, М.И. Сниегс. – Рига, Зинтане, 1980. – 182с.

33. Расчеты на прочность в машиностроении. / Справочник в 3-х томах. Под ред. С.Д. Пономарева, В.Л. Бидермана, К.К. Лихарева.// Т.2. – М.: Машиностроение, 1958 – 974с.

34. Розин Л.А., Константинов И. А., Смелов В. А. Расчет статически неопределимых стержневых систем: Учеб. пособие. – Л.: Издательство Ленинградского университета. 1987. 328 с.

35. Сборник задач по сопротивлению материалов/Под ред. А. С. Вольмира. – М.: Наука, Главная редакция физико-математической литературы, 1984. – 408 с.

36. Светлицкий В. А. Механика стержней: Учеб. для втузов. В 2-х ч. Ч. I. Статика. – М.: Высш. шк., 1987. – 320 с.: ил.

37. Светлицкий В. А. Механика стержней: Учеб. для втузов. В 2-х ч. Ч. II. Динамика. – М.: Высш. шк., 1987. – 304 с.: ил.

38. Сегерлинд Л. Применение методов конечных элементов. Москва; Изд-во «Мир», 1979.

39. Справочник по математике для инженеров и учащихся втузов. Издание переработанное. Под ред. Г. Гроше и В. Циглера. Издв-во «Тойбнер», Лейпчиг, 1979. Москва «Наука», Главная редакция физ.-мат.литературы, 1980.

40. Тимошенко С. П. Сопротивление материалов. Перевод В.Н. Федорова с 3его амер. издания. Гос. изд-во физ.-мат. лит-ры. Москва. 1960.

41. Товстик П.Е. Асимптотический метод интегрирования уравнений колебаний пружин. –Вестник ЛГУ. Математика, механика, астрономия. Вып.27. – Л.: ЛГУ, 1963.

42. Товстик П.Е. Вынужденные колебания плоских пружин. // В кн.Исследования по упругости и пластичности. Вып.3. – Л.: ЛГУ, 1963.

43. Хвингия М.В. Вибрации пружин. – М.: Машиностроение, 1969 – 286с.

44. Хечумов Р. А., Кеплер Х., Прокофьев В. И. Применение метода конечных элементов к расчету конструкций. Изд-во ассоциации строительных вузов. Москва, 1994.

45. Черных К. Ф. Нелинейная теория упругости в машиностроительных расчетах». Ленинградское отделение ордена Трудового Красного Знамени издательства «Машиностроение». 1985 г.

46. Яблонский А. А., Никифорова В. М. Курс теоретической механики. Ч.I. Статика.

47. Фаддеев Д.К., Фаддеева В.Н. Вычислительные методы линейной алгебры. – М.-Л.: Физматгиз, 1963. – 734с

 

[1] Буква  используется для обозначения произвольной скалярной величины. Буквы  и  применяются соответственно для обозначения температуры и давления, когда речь идет о конкретных приложениях.

[2]Для того, чтобы компоненты деформаций образовывали тензор, необходимо правые части выражений , ,  умножить на ½.