Конечный элемент стержня в локальной системе координат.

Благодаря тому, что выбранная система координат включает в себя главные центральные оси инерции поперечного сечения, вариационный функционал Лагранжа можно разделить на 4 части, каждая из которых будет включать в себя единственную искомую функцию

                 (3.3.1) (растяжение/сжатие)

                     (3.3.2) (кручение)

               (3.3.3)                 

(оба изгиба в главных плоскостях поперечного сечения).

В силу независимости вариационных уравнений (3.3.1 – 3.3.3) четыре сформулированные уравнения можно решать раздельно. [1]

Рис.8

Простейшей формой конечного элемента является стержень с двумя узлами.

1) При выборе функции формы для такого конечного элемента ограничимся полиномами, степень которых обеспечивает ненулевые производные необходимого порядка: для растяжения/сжатия и кручения минимальная степень полинома равна 1, для изгиба - 2.

v(x) = u₁(1 – x/l) + u₂x/l -                для растяжения/сжатия            (3.3.4)

j(x) = j₁(1 – x/l) + j₂x/l -        для кручения

Для изгиба удобнее выбирать полиномы третьей степени, причем в качестве основных неизвестных следует задавать поперечные перемещения узлов и углы поворота узловых сечений. [13]

v(x) = a₀ + a₁x + a₂x² + a₃x³

v(x) = v₁ P₁(x) + J₁lP₂(x) + v₂ P₃(x) + J₂lP₄(x)

 

P₁(x) = 1 - 3x² + 2x²,    где x = x/l

P₂(x) = x(1 - x)²

P₃(x) = x²(2 - 3x)

P₄(x) = x²(x - 1)                                          (3.3.5)

Матрица градиентов для этих случаев представляет собой скалярные операторы:

Вектор деформации:

Работа внутренних сил при растяжении:

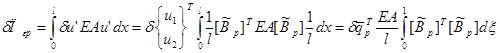
Матрица жесткости в локальных координатах:

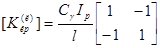
Для плоского изгиба матрица дифференциальных операторов имеет вид

Матрица градиентов функции форм:

Матрица жесткости при изгибе:

                      

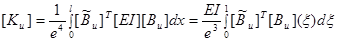
              (3.3.6)

Момент инерции в этой формуле выбирается в зависимости от плоскости изгиба.

Рассмотрим элементарную работу распределенных нагрузок. Для растяжения/сжатия

Если нагрузка p_x постоянна, то выражение для вектора х можно вычислить аналитически

Рис.9

Вектор узловых сил:

 

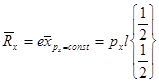
2) Важным частным случаем растяжения является растяжение или сжатие собственным весом.

Sx = -N(x) + rgAx = 0

N(x) = rgAx

N_x(0) = 0;    N_x(l) = rgAl

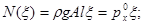 где

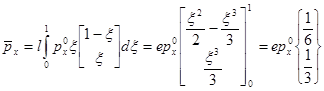
Введенные расчетные формулы пригодны и для кручения, только в них под распределенной нагрузкой следует понимать распределенный крутящий момент m_x, а вектор узловых нагрузок будет состоять из двух крутящих моментов, приложенных в узлах конечных элементов в статически эквивалентных к распределенному моменту.

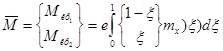           (3.3.7)

При изгибе распределенная поперечная нагрузка совершает элементарную работу:

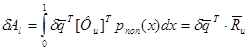
`R_u - вектор узловых поперечных сил и изгибающих моментов

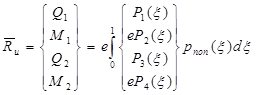                         (3.3.8)

Нагрузка p_non есть либо p_y либо p_z в зависимости от плоскости изгиба.

Рассмотрим физический смысл компонент матрицы жесткости. С этой целью запишем уравнение состояния одного конечного элемента:

[k]`q = `R

В соответствии с этой формулой можно утверждать, что произведение [k]`q имеет размерность силы; так как `R внешняя сила, то указанное произведение есть внутренняя сила и уравнение состояния имеет смысл уравнения равновесия. [11]

Поясним физический смысл компонент матрицы жесткости на примере конечного элемента стержня, работающего на плоский изгиб.

Рис.10а

 

q₃ = v₂ = 0

q₄ = Q₂ = 0

q₂ = Q₁ = 0

`q⁽¹⁾ = {1; 0; 0; 0}

Q₁ = K₁₁

M₁ = K₁₂

Q₂ = K₁₃

M₂ = K₁₄

Физический смысл коэффициентов матрицы жесткости следующий: диагональная компонента матрицы жесткости равна внешней нагрузке, которую следует приложить к одному из узлов конечного элемента в схеме закрепления конечных элементов, когда у выбранного узла свободной является только одна из степеней свободы; внешняя нагрузка, соответствующая этой степени свободы должна обеспечивать перемещение, равное единице. Все остальные внедиагональные компоненты равны опорным реакциям, возникающим в этой схеме закрепления. [17]

Рис.10б

Из физического смысла компонент матрицы жесткости следует положительность диагональных коэффициентов и из теоремы взаимности перемещения – симметрии матрицы. Ранг матрицы жесткости равен разности между количеством степеней свободы конечных элементов (количество компонент вектора узловых перемещений) и количеством степеней свободы конечных элементов как абсолютно твердого тела.

Все приведенные рассуждения относились к локальной координатной системе, связанной с конечными элементами.

Рис.11

Сборка конечных элементов в единый ансамбль (конечно-элементную модель стержневой системы) производится в неподвижной системе, чаще всего декартовых координат.

Рассмотрим возможные способы пересчета перемещения стержня из локальных в глобальные координаты.

Взаимное расположение двух систем координат характеризуется одним параметром

`u = u<sub>x</sub>`x⁰ + u_h`h<sup>0</sup> = u<sub>x</sub>`x₀ + u_y`y₀               

u_x = u_x`x<sub>0</sub> × `x₀ + u_y`y<sub>0</sub> ×`x₀                     | × `x⁰

u_h = u_x`x<sub>0</sub> × `h₀ + u_y`y<sub>0</sub> ×`h₀                     | × `h⁰

В матричной форме это уравнение имеет вид:

`u<sup>(л)</sup> = [cos]`u^(г)

                                                                         (3.3.9)

 [cos] – матрица направляющих косинусов в глобальной и локальной системе координат. Для пересчета вектора узловых перемещений в глобальные координаты отметим, что он составляется из векторов перемещений узлов, следовательно, каждый из этих векторов должен преобразовываться независимо от другого. [10] Тогда матрица преобразования вектора узловых перемещений будет блочно-диагональной

                                 (3.3.10)

Здесь n, n+1 – номера узлов конечного элемента; диагональные подматрицы определены формулой (3.3.9). Для прямого стержня диагональные подматрицы одинаковы, для криволинейного стержня могут быть разными. Тогда формула пересчета вектора узловых перемещений из локальных координат в глобальные может быть записана следующим образом

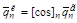
(d`q<sup>г</sup>)<sup>T</sup>[сos]<sup>T</sup>{[K][с os]`q^г  -`R^л} = 0

(d`q<sup>г</sup>)<sup>T</sup>{[K<sup>г</sup>]`q^г - `R^г} = 0

Последнее выражение переводит матрицу жесткости с индексом m из локальных в глобальные координаты.

Матрица жесткости одного конечного элемента имеет вид (см. Приложение 1)

                                  (3.3.11)

Эта формула пересчитывает вектор узловых нагрузок из локальных в глобальные координаты.

Вектор узловых нагрузок имеет следующий вид: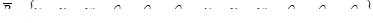

Разрешающее уравнение МКЭ в глобальных координатах – система равновесия (или движения) узлов конечных элементов в проекциях на оси глобальной системы координат.

Для конечного элемента стержня в пространственной системе координат рассуждения полностью сохраняются; отличия заключаются в том, что и локальная и глобальная системы координат являются трехмерными и исходным для вывода матрицы направляющих косинусов является тождество

u _x ` x <sup>0</sup> + u <sub>h</sub> ` h ⁰ + u _V ` V <sup>0</sup> = u<sub>x</sub> ` x₀ + u_y ` y<sub>0</sub> + u<sub>z</sub> ` z₀.

u_x = u_x`x<sub>0</sub> × `x₀ + u_y`y<sub>0</sub> ×`x₀  + u_z`z<sub>0</sub> ×`x₀            

u_h = u_x`x<sub>0</sub> × `h₀ + u_y`y<sub>0</sub> ×`h₀ + u_z`z<sub>0</sub> ×`h₀      

u_z = u_x`x<sub>0</sub> × `z₀ + u_y`y<sub>0</sub> ×`z₀ + u_z`z<sub>0</sub> ×`z₀                        

Скалярное произведение единичных векторов локальных и глобальных координат могут быть выражены через три независимых угла Эйлера. [10]

 

Используем матрицу направляющих косинусов, имеющую следующий вид (здесь углы Эйлера обозначены через j, y, q):    [8]

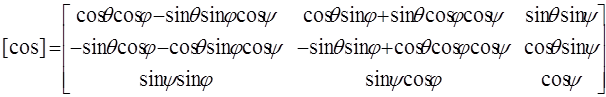
Матрица перехода от локальных координат к глобальным для криволинейного стержня будет иметь вид

где

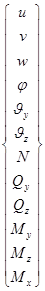 - вектор узловых перемещений в локальных координатах.

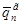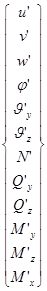= - вектор узловых перемещений в глобальных координатах

Здесь u , v , w – компоненты вектора перемещений, j - угол закручивания, - углы поворота поперечного сечения относительно главных центральных осей инерции, N – продольная сила, Q_y , Q_z – поперечные силы, М _x , M_y , M_z – моменты.

Если соединение конечных элементов в ансамбль осуществляется по всем степеням свободы узлов и деформации системы малы, то матрицу направляющих косинусов можно считать постоянной; в противном случае необходимо учитывать возможность конечных поворотов локальной координатной системы относительно глобальной. В этом случае в качестве независимых параметров, определяющих взаимную ориентацию координатных систем вместо углов Эйлера удобнее использовать параметры Родрига-Гамильтона.

Удобство заключается в том, что упомянутые параметры связаны с угловой скоростью вращения локальной координатной системы относительно глобальной квазилинейным дифференциальным уравнением первого порядка. [30]