 |
Главная |
Методика изучения темы «Преобразование тригонометрических выражений».
|
из
5.00
|
В настоящее время все чаще используют инновационные технологии образования. Одним из вариантов является кейс-технология. Причем, ее использование возможно в сочетании с другими образовательными технологиями.
На основе проведенного исследования А. Долгоруким были выделены следующие этапы применения кейс-технологии на уроках математики: 1) подготовка и предоставление учителем учебно-методического материала по изучаемой теме каждому ученику; 2) планомерная и последовательная работа с учащимися по проработке каждого вопроса темы, предполагающая как самостоятельное изучение ребенком отдельных вопросов, так и работу в классе или индивидуальные консультации; 3) обязательное обобщение изучаемой темы учителем, выявление пробелов в изучении отдельных вопросов темы и их устранение; 4) диагностика по окончании изучения темы или раздела.
В соответствии с тематическим планированием составлено 13 фрагментов уроков по теме «Преобразование тригонометрических выражений», которые были реализованы в урочное время. 4 фрагмента по изучению нового материала, 4 – на закрепление, 1 – на актуализацию знаний, 4 – самостоятельных и контрольных работ.
На этапе контроля знаний проверяются уровни сформированности познавательного интереса с помощью умений решать кейсы, на этапах изучения нового материала, актуализации знаний и закреплении формируются уровни познавательного интереса и уровни умений решать кейсы.
Были разработаны следующие методические схемы применения кейс метода, направленные на формирование познавательного интереса.
§ Методическая схема решения кейс-заданий 1 уровня.
| Деятельность учителя | Деятельность учащихся |
| 1. Предлагает практический пример. 2. Создает ситуацию. 3. Предлагает систему вопросов для анализа ситуации. 4. Подводит учащихся к формулированию проблем. 5. Следит за отбором проблем. 6. Руководит поиском решения проблемы. 7. Решает ситуацию. | 1. Рассматривают пример. 2. Внимательно слушают. 3. Анализируют ситуацию. 4. Выдвигают гипотезы по определению возможных проблем. 5. Выделяют основную проблему. 6. Находят пути решения проблемы. 7. Решают ситуацию. |
Фрагмент урока №1 по теме «Формулы двойного аргумента» (25.11.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные: изучить формулы двойного аргумента и отработать умения по их применению;
воспитательные: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: изучение нового материала.
| Деятельность учителя | Деятельность учащихся | Вид доски |
- Перейдем к изучению нового материала. Откройте тетради, запишите число и тему урока «Формулы двойного аргумента».
( предлагает практический пример и создает ситуацию )
- На доске записаны тригонометрические функции.
(предлагает систему вопросов для анализа ситуации)
- Что можно с ними сделать?
- По каким признакам мы можем их классифицировать?
- Что у нас получится?
- Еще?
- Что получится?
(подводит учащихся к формулированию проблем)
- Какие аргументы у нас получились в каждом столбике?
- Обратите внимание на последний столбик.
- Как вы думаете, что нам нужно сделать с этими выражениями?
(анализ данных)
- Рассмотрим выражение  .
- Как называется в данном выражении?
(выдвижение гипотез)
- Как мы можем представить ?
- Как дальше можем преобразовать?
- Правильно.
(решение проблемы)
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Перепишите еще раз начало и конец, и обведите в рамочку.
(анализ полученных результатов)
- Таким образом, что мы получили?
- Аналогично выводится формула для .
- Как называется в данном выражении?
(выдвижение гипотез)
- Как мы можем представить ?
- Как дальше можем преобразовать?
- Правильно.
(решение проблемы)
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Перепишите еще раз начало и конец, и обведите в рамочку.
(анализ полученных результатов)
- Таким образом, что мы получили?
- Аналогично выводится формула для 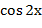 .
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Запишите формулу и обведите в рамочку.
(анализ данных)
- В виде чего представлена данная формула?
(выдвижение гипотез)
- Можно ли представить формулу так, чтобы она содержала в правой части только синус?
- Как?
- Что получится? Диктуйте. (решение проблемы)
- Запишите формулу и обведите в рамочку.
- Можно ли представить формулу так, чтобы она содержала в правой части только косинус?
- Как?
- Запишите каждый у себя в тетрадях. А Лашкевич Ольга запишет на доске.
- Молодец. Садись.
- Запишите формулу и обведите в рамочку.
- А для .
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Запишите формулу и обведите в рамочку.
(анализ данных)
- В виде чего представлена данная формула?
(выдвижение гипотез)
- Можно ли представить формулу так, чтобы она содержала в правой части только синус?
- Как?
- Что получится? Диктуйте. (решение проблемы)
- Запишите формулу и обведите в рамочку.
- Можно ли представить формулу так, чтобы она содержала в правой части только косинус?
- Как?
- Запишите каждый у себя в тетрадях. А Лашкевич Ольга запишет на доске.
- Молодец. Садись.
- Запишите формулу и обведите в рамочку.
- А для  выведет формулу …..?
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Перепишите еще раз начало и конец, и обведите в рамочку.
- Таким образом, мы с вами вывели три формулы двойного аргумента.
- Скажите, пожалуйста, для каких значений аргумента справедливы формулы синуса двойного аргумента и косинуса двойного аргумента?
- Правильно. А для каких значений аргумента справедлива формула тангенса двойного аргумента?
- Какое здесь еще существует необходимое условие?
- Данные формулы можно применять как справа налево, так и слева направо.
- Разумеется, формулы двойного аргумента можно применять и в тех случаях, когда место аргумента выведет формулу …..?
Учитель вызывает одного ученика к доске.
- Молодец. Садись. Перепишите еще раз начало и конец, и обведите в рамочку.
- Таким образом, мы с вами вывели три формулы двойного аргумента.
- Скажите, пожалуйста, для каких значений аргумента справедливы формулы синуса двойного аргумента и косинуса двойного аргумента?
- Правильно. А для каких значений аргумента справедлива формула тангенса двойного аргумента?
- Какое здесь еще существует необходимое условие?
- Данные формулы можно применять как справа налево, так и слева направо.
- Разумеется, формулы двойного аргумента можно применять и в тех случаях, когда место аргумента  занимает более сложное выражение.
- Может, вы скажете сразу, без вычислений, чему равен занимает более сложное выражение.
- Может, вы скажете сразу, без вычислений, чему равен  ?
- Правильно. Молодцы. ?
- Правильно. Молодцы.
|
(рассматривают пример)
(анализируют ситуацию)
- Классифицировать.
- По названию функций.
Дети классифицируют.
- По аргументу.
Дети классифицируют.
(выдвигают гипотезы по определению возможных проблем)
- В первом столбике – единичный аргумент, во втором – половинный, в третьем – двойной.
- Вывести формулы.
(анализируют данные)
- Аргументом.
(выдвигают гипотезу)
- Как  .
- По формуле синуса суммы.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- .
- По формуле синуса суммы.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- 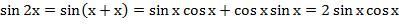 . .
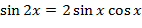 - Мы вывели формулу двойного аргумента для синуса.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
-
- Мы вывели формулу двойного аргумента для синуса.
Один ученик выходит к доске. Остальные выполняют в тетрадях.
- 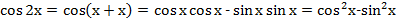 . .
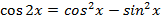 (анализируют данные)
- В виде двух тригонометрических функций.
(выдвигают гипотезу)
- Да.
- Выразить
(анализируют данные)
- В виде двух тригонометрических функций.
(выдвигают гипотезу)
- Да.
- Выразить 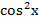 по основному тригонометрическому тождеству.
- по основному тригонометрическому тождеству.
-  . .
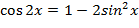 - Да.
- Тоже по тригонометрическому тождеству.
Лашкевич Ольга выходит к доске и записывает:
-
- Да.
- Тоже по тригонометрическому тождеству.
Лашкевич Ольга выходит к доске и записывает:
- 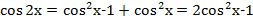 . .
 Один ученик выходит к доске. Остальные выполняют в тетрадях.
-
Один ученик выходит к доске. Остальные выполняют в тетрадях.
-  . .
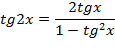 - Для любых значений аргумента.
- Для тех значений аргумента
- Для любых значений аргумента.
- Для тех значений аргумента  , для которых определены , для которых определены 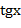 и и  .
- Знаменатель должен быть не равен нулю.
- .
- Знаменатель должен быть не равен нулю.
- 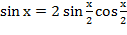 . .
| Задание № 1.
 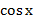
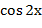 
 
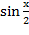 

 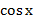 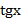
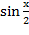  
 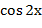 
 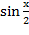 
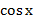  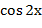
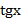  
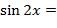
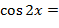
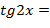
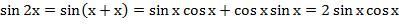 . .
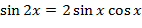
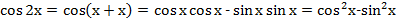 . .
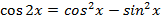
 . .
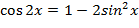
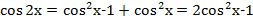 . .

 . .
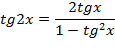
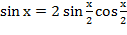 . .
|
§ Методическая схема решения кейс-заданий 2 уровня.
| Деятельность учителя | Деятельность учащихся |
| 1. Создает ситуацию. 2. Подводит учащихся к формулированию проблем. 3. Руководит отбором проблем. 4. Руководит поиском решения проблемы. 5. Решает ситуацию. | 1. Внимательно слушают, анализируют ситуацию. 2. Выдвигают гипотезы по определению возможных проблем. 3. Выделяют основную проблему. 4. Находят пути решения. 5. Решают ситуацию. |
Фрагмент урока №2 по теме «Формулы двойного аргумента» (25.11.2009г).
Тип урока: закрепление.
Цели:
образовательные: отработать умения по применению формул двойного аргумента;
воспитательные: воспитать внимание, умение отвечать на вопросы, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, формирование познавательного интереса к математике.
Этап урока: закрепление.
| Деятельность учителя | Деятельность учащихся | Вид доски |
(создает ситуацию)
- Даны корни уравнения 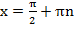 и и  .
(подводит учащихся к формулированию проблем)
- Что мы можем с ними сделать?
- Каким должно быть уравнение?
- А еще каким?
(анализ данных)
- Какое это будет уравнение, простейшее или сложное?
- А как вы определили, что оно сложное?
(выдвижение гипотез)
- В каком случае можно приравнять уравнения?
(поиск путей решения и решение проблемы)
- Какое мы можем составить первоначальное уравнение?
- Мы можем оставить такое уравнение?
- Дальше что нужно?
- Мы можем ее применить?
- Почему?
- Что получится?
- Что получим?
- Подобное задание будет в самостоятельной работе. .
(подводит учащихся к формулированию проблем)
- Что мы можем с ними сделать?
- Каким должно быть уравнение?
- А еще каким?
(анализ данных)
- Какое это будет уравнение, простейшее или сложное?
- А как вы определили, что оно сложное?
(выдвижение гипотез)
- В каком случае можно приравнять уравнения?
(поиск путей решения и решение проблемы)
- Какое мы можем составить первоначальное уравнение?
- Мы можем оставить такое уравнение?
- Дальше что нужно?
- Мы можем ее применить?
- Почему?
- Что получится?
- Что получим?
- Подобное задание будет в самостоятельной работе.
|
(выдвигают гипотезы по определению возможных проблем и выделяют основную проблему)
- Найти уравнение, которому принадлежат эти корни.
- Тригонометрическим.
- На тему урока.
(анализируют данные)
- Сложное.
- Будет состоять из двух простейших.
- Первому корню соответствует уравнение  . Второму – . Второму –  .
(выдвигают гипотезу)
- Когда оба уравнения равны нулю.
- .
(выдвигают гипотезу)
- Когда оба уравнения равны нулю.
- 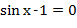 .
- .
- 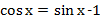 -
- 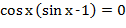 .
- Да, но можем раскрыть скобки.
- .
- Да, но можем раскрыть скобки.
- 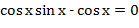 - Так как уравнение должно быть на тему урока, то нужно применить формулу двойного аргумента.
- Нет.
- Можно было применить, если бы перед
- Так как уравнение должно быть на тему урока, то нужно применить формулу двойного аргумента.
- Нет.
- Можно было применить, если бы перед 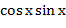 стояла двойка.
- Нужно домножить обе части уравнения на 2.
- . Отсюда, свернув по формуле синуса двойного аргумента, получим стояла двойка.
- Нужно домножить обе части уравнения на 2.
- . Отсюда, свернув по формуле синуса двойного аргумента, получим
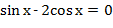 . .
| Задание № 2.
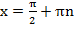

 . .
 . .
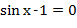 . .
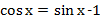 . .
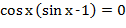 . .
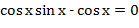 .
. .
.
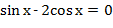 . .
|
§ Методическая схема решения кейс-заданий 3 уровня.
| Деятельность учителя | Деятельность учащихся |
| 1. Создает ситуацию. 2. Подводит учащихся к формулированию проблем. 3. Руководит отбором проблем. 4. Следит за правильностью рассуждений. 5. Подводит учащихся к выбору оптимального пути решения. 6. Решает ситуацию. | 1. Внимательно слушают, анализируют ситуацию. 2. Выдвигают гипотезы по определению возможных проблем. 3. Выделяют основную проблему. 4. Предлагают концепцию решений. 5. Выбирают из всевозможных предложений оптимальный путь решения. 6. Решают ситуацию. |
Фрагмент урока №5 по теме «Преобразование суммы тригонометрических функций в произведение» (02.12.2009г).
Тип урока: изучение нового материала.
Цели:
образовательные: повторить ранее изученный материал;
воспитательные: воспитать внимание, активно участвовать в беседе, аргументировать свою точку зрения, умение слушать других;
развивающие: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения проблемы, формирование познавательного интереса к математике.
Этап урока: актуализация знаний.
| Деятельность учителя | Деятельность учащихся | Вид доски |
| - Поработаем устно. (создает ситуацию, подводит учащихся к формулированию проблем) - Что вы видите на доске? - А еще? - Что это за формулы? - Как вы думаете, зачем они записаны на доске? - У кого есть другие варианты? - Какую задачу мы поставим перед собой? (решение проблемы) - Есть ли в первой формуле ошибки? - Правильно. А во второй формуле? - Правильно. В третьей формуле? - В четвертой? - А в пятой? - Правильно. В шестой формуле? - Есть ли ошибка в седьмой формуле? - В восьмой формуле? - В девятой? - В десятой? - В одиннадцатой формуле? - И в последней формуле? - Молодцы! |
(выдвигают гипотезы по определению возможных проблем и выделяют основную проблему)
- Равенства.
- Формулы.
- Преобразования тригонометрических выражений.
- Чтобы вспомнить, и легче было решать задания.
- В них допущены ошибки.
- Необходимо найти ошибки.
(поиск путей решения и решение проблемы)
- В первой формуле в правой части надо поменять знак на «+» и поменять функции 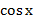 и и  местами.
- Во второй формуле между функциями местами.
- Во второй формуле между функциями  и и 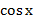 должен стоять знак « должен стоять знак « 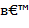 ».
- В третьей формуле в знаменателе между ».
- В третьей формуле в знаменателе между 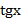 и и 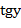 стоит знак умножения.
- В четвертой формуле в числителе вместо знака «+» надо поставить знак «-» и поменять стоит знак умножения.
- В четвертой формуле в числителе вместо знака «+» надо поставить знак «-» и поменять  на на 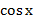 .
- В пятой формуле надо поменять функции .
- В пятой формуле надо поменять функции  и и 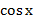 местами.
- В шестой формуле надо поменять числитель и знаменатель местами.
- В седьмой формуле надо в правой части поменять знак на «-».
- В восьмой формуле в правой части нет двойки и надо поменять местами.
- В шестой формуле надо поменять числитель и знаменатель местами.
- В седьмой формуле надо в правой части поменять знак на «-».
- В восьмой формуле в правой части нет двойки и надо поменять 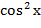 и и 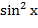 местами.
- В девятой формуле все верно.
- В десятой формуле тоже все верно.
- В одиннадцатой формуле в числителе между местами.
- В девятой формуле все верно.
- В десятой формуле тоже все верно.
- В одиннадцатой формуле в числителе между 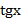 и и 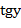 стоит знак «-», а в знаменателе после 1 стоит знак «+».
- В двенадцатой формуле в числителе должно быть . стоит знак «-», а в знаменателе после 1 стоит знак «+».
- В двенадцатой формуле в числителе должно быть .
| Задание № 7.
 2)
2)  3)
3) 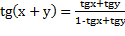 4)
4) 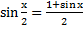 5)
5)  6)
6) 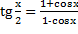 7)
7)  8)
8)  9)
9)  10)
10) 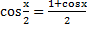 11)
11) 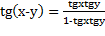 12)
12) 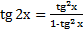
|
§ Методическая схема решения кейс-заданий 4 уровня.
| Деятельность учителя | Деятельность учащихся |
| 1. Создает ситуацию. 2. Подводит учащихся к формулированию проблем. 3. Руководит отбором проблем. 4. Следит за правильностью рассуждений. 5. Подводит учащихся к выбору оптимального пути решения. 6. Следит за процессом решения. | 1. Внимательно слушают, анализируют ситуацию. 2. Выдвигают гипотезы по определению возможных проблем. 3. Выделяют основную проблему. 4. Предлагают концепцию решений. 5. Выбирают из всевозможных предложений оптимальный путь решения. 6. Решают ситуацию. |
Фрагмент урока №8 по теме «Преобразование произведения тригонометрических функций в сумму» (14.12.2009г).
Тип урока: закрепление.
Цели:
образовательные: закрепить формулы преобразования произведения тригонометрических функций в сумму и отработать умения по их применению;
воспитательные: воспитать внимание, умение работать самостоятельно;
развивающие: сформировать умения анализировать данные, выдвигать гипотезы по определению основной проблемы, находить оптимальные пути решения, решать проблему, формирование познавательного интереса к математике.
Этап урока: самостоятельная работа.
| Деятельность учителя | Деятельность учащихся | Вид доски |
| ( создает ситуацию ) - А сейчас самостоятельная работа. Подпишите листочки и номер варианта. Я раздам вам карточки. Каждая карточка содержит по 4 задания. Первые три задания общего характера. Четвертое задание творческого характера на отдельную оценку. В первом задании необходимо представить выражение в виде суммы, во втором – вычислить, в третьем – решить уравнение. В четвертом задании – дано выражение. Ваша задача сформулировать задание и решить его. Время для работы 20 минут. Критерии оценивания: 3 правильно решенных задания на «5», 3 задания с недочетами - «4», 2 задания на «3» и соответственно меньше двух заданий «2». Время пошло. Приступаем к выполнению заданий. | (рассматривают пример, анализируют ситуацию, выдвигают гипотезы по определению возможных проблем и выделяют основную проблему, находят пути решения и решают ситуацию) | Задание № 11.
Дано выражение
 .
Сформулируйте задание и решите. .
Сформулируйте задание и решите.
|
Данное кейс-задание учащиеся выполняют самостоятельно.
В самостоятельной работе первые три задания общего характера, 4 задание – на формирование I, II, III и IV уровней познавательного интереса.
Самостоятельная работа.
Вариант 1.
1. Представьте в виде суммы:
 .
2. Вычислите: .
2. Вычислите:
 .
3. Решите уравнение: .
3. Решите уравнение:
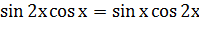 .
4*. Дано выражение .
4*. Дано выражение
 .
Сформулируйте задание и решите. .
Сформулируйте задание и решите.
| Самостоятельная работа.
Вариант 2.
1. Представьте в виде суммы:
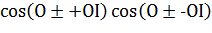 .
2. Вычислите: .
2. Вычислите:
 .
3. Решите уравнение: .
3. Решите уравнение:
 .
4*. Дано выражение .
4*. Дано выражение
 .
Сформулируйте задание и решите. .
Сформулируйте задание и решите.
|
Общие критерии оценивания первых трех заданий:
«5» - верно выполненные 3 задания.
«4» - 3 задания с недочетами.
«3» - 2 задания.
«2» - менее 2 заданий.
Критерии оценивания кейс-задания:
1. Правильно сформулировано задание.
2. Правильно выполнены преобразования.
3. Применение формул преобразования тригонометрических выражений.
4. Найдено уравнение.
«2» - менее 2 пунктов (I уровень).
«3» - 2 пункта (II уровень).
«4» - 3 пункта (III уровень).
«5» - 4 пункта (IV уровень).
Вывод: Во второй главе выделены цели изучения темы «Преобразования тригонометрических выражений», классификация кейс-заданий, формирующая умения решать кейсы и уровни познавательного интереса. Составлено тематическое планирование. Разработана система заданий и методика работы над ними.
Глава 3.
|
из
5.00
|
Обсуждение в статье: Методика изучения темы «Преобразование тригонометрических выражений». |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

