Автоматизированные системы плазовых работ

С появлением и развитием вычислительной техники стали использовать аналитические методы для проектирования формы корпуса судна и для выполнения плазовых работ.

В Российском и зарубежном судостроении разработаны и применяют системы автоматизированного проектирования судов (САПР). В состав этих систем входят подсистемы, решающие плазовые задачи математическими методами на основе математических моделей формы и конструкции корпуса судна. Подсистемы содержат модули, каждый из которых решает определенную задачу.

В России для автоматизированного решения плазовых задач используются отечественные системы, например, РИТМ-Судно и зарубежные системы FORAN, TRIBON, CATIA, AVEVA.

Плазовые модули всех систем решают идентичные задачи и выдают аналогичные результаты. Они различаются применяемым математическим аппаратом и структурой программного обеспечения.

Принципиальная структура модулей автоматизированной системы решения плазовых задач, присущая большинству существующих САПР судов, содержит:

- банк исходных данных (исходной информации);

- математическую модель (систему математических уравнений, описывающих геометрию корпуса);

- математический метод (алгоритм) решения задачи;

- программы решения задачи;

- расчетные материалы и алгоритмы для решения задач;

- результаты решения;

- графические и текстовые представления результатов решения, выполняемые чертежными машинами и печатающими устройствами.

Модулями подсистемы плазовых задач рассчитываются и вычерчиваются:

- теоретическая форма корпуса (генерируются его теоретические обводы и вычерчивается теоретический чертеж);

- положения теоретических линий пазов, стыков наружной обшивки, поперечного и продольного набора (генерируются его теоретические линии и вычерчивается практический корпус);

- контуры и размеры плоских деталей и разверток гнутых деталей корпусных конструкций и вычерчиваются эскизы деталей и разверток;

- раскрой листового и профильного проката и вычерчиваются карты раскроя;

- разрабатываются корпусные конструкции и вычерчиваются корпусные сборочные чертежи;

- контуры и размеры гибочных шаблонов для проверки формы изогнутых деталей в процессе их гибки;

- контуры и размеры оснастки, необходимой для сборки и проверки корпусных конструкций и корпуса в целом;

- управляющие программы тепловой резки листового проката для машин с ЧПУ.

Для расчета формы и размеров деталей корпуса необходимы дополнительные исходные данные о конструкциях корпуса, положении палуб и переборок, продольного и поперечного набора, форме оконечностей, размерах связей. Данные берутся из рабочих чертежей или из современных САПР, в которых имеются модули, проектирующие и вычерчивающие конструкции корпуса.

Плазовые работы начинаются с построения судовой поверхности формы корпуса судна.

Исходными данными для генерирования теоретической формы корпуса судна служат главные размерения судна, проектные характеристики формы корпуса (коэффициенты полноты, погибь бимсов, седловатость палуб и другие).

Форма корпуса судна может быть представлена в аналитическом виде как математическая модель. Применяются три формы математических моделей: цифровая, аппроксимационная и чисто математическая.

В цифровой модели обводы корпуса представляются в виде таблиц ординат к теоретическому чертежу и практическому корпусу (плазовая книга). Аппроксимационная модель задает обводы в виде семейства математических кривых, коэффициенты которых определяются по данным цифровой модели. Чисто математическая (каркасная) модель – это семейство уравнений кривых и поверхностей корпуса, задаваемых в процессе формирования этой модели.

В аппроксимационной модели одной из основных задач построения обводов корпуса является трассировка - определение координат точек пересечения пазов и теоретических линий продольного набора с линиями шпангоутов. Для решения этой задачи необходимо знать уравнения линий шпангоутов и продольных теоретических линий пазов и набора. 

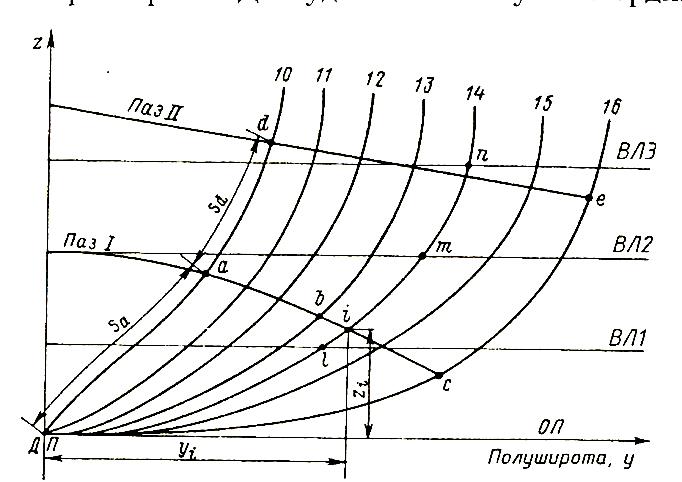
Рис. 2.11. Фрагмент проекции «корпус» с прямолинейным

и криволинейным пазами.

Уравнения шпангоутов задаются в виде параболы

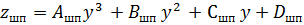
Уравнение криволинейного паза

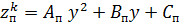
Уравнение прямого паза

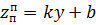
Для нахождения коэффициентов в уравнениях необходимо определить координаты четырех точек, принадлежащих шпангоуту (l, i, m, n) , а также точек криволинейного паза (a,b,c) – см. рис.2.11.

Для прямолинейного паза

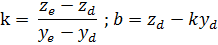
При задании точек пересечения в виде криволинейных координат длинами дуг 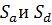   при нахождении координаты y необходимо определить значение

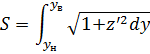
Координаты у точек а, в, с определяются как верхний предел этого интеграла, по которому определяется длина дуги шпангоута между пазами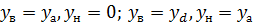

При построении практического корпуса на основе математической модели выполняется согласование и сглаживание обводов корпуса с использованием разностей таблично заданных функций или кубических сплайнов.

Согласование и сглаживание теоретических кривых обводов корпуса при задании теоретических кривых в виде цифровой таблично заданной функции можно выполнить по математическому аппарату конечных или разделенных разностей, которые по своим свойствам аналогичны свойствам производных. Конечная разность - это разность цифровых значений координат рядом расположенных точек кривых обводов корпуса.

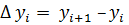
 Разделенная разность представляет    отношение конечных разностей координат рядом расположенных точек на кривой точек.

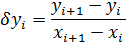
Для ватерлиний или шпангоутов с равноотстоящими полуширотами применяются конечные разности, а с не равноотстоящими полуширотами – разделенные разности.

Конечные разности используются для оценки плавности кривых обводов корпуса по следующим критериям:

-первые и вторые разности должны плавно возрастать или убывать;

-вторые разности не должны менять знака.

В том случае если вторые разности возрастают или убывают монотонно, то это свидетельствует о наличии скрытой волнистости линии обвода корпуса.

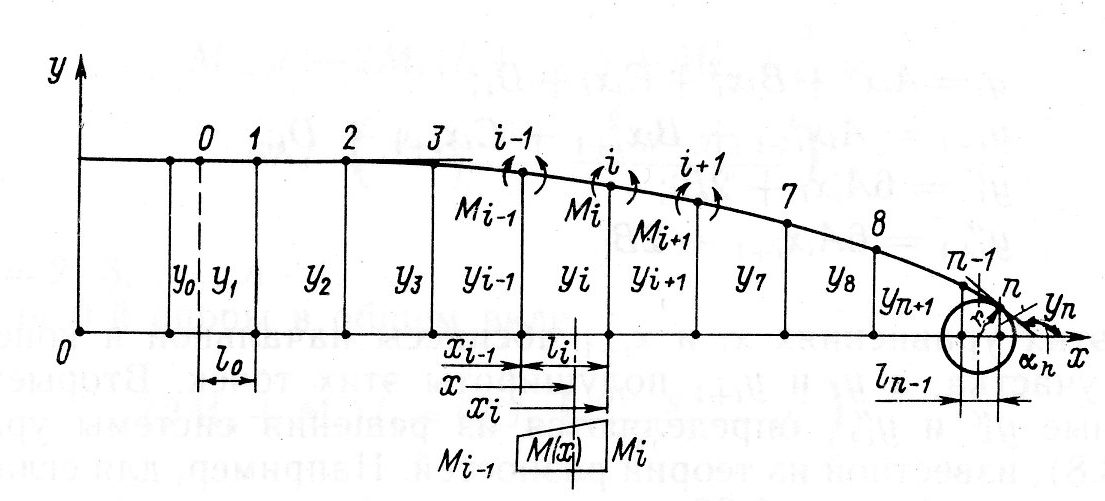
Рис. 2.12. Носовая ветвь ватерлинии.

 Согласование и сглаживание обводов с использованием кубических сплайнов основано на физической аналогии пружинения участков гибкой рейки, не лежащих на плавной кривой, при снятии того или иного груза прижимающего рейку к основанию. Для участков рейки, лежащих на плавной кривой, величина пружинения равна 0, а на других участках – равна ±ε_i. Для определения этой величины рассматривается многопролетная балка постоянного сечения со смещенными абсолютно жесткими опорами, нагруженная внешней нагрузкой. Для этой балки составляется система уравнений трех моментов.

Для i-ой опоры:

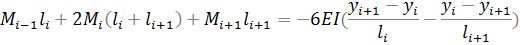
Для нулевой опоры:

 -

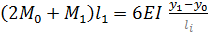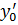
Для n -ной опоры

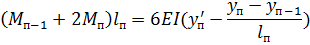
Ватерлиния в точке 0 плавно сопрягается с участком цилиндрической вставки и 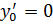. В точке n производная 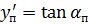. Эти граничные условия соответствуют жесткой заделке изогнутой по ватерлинии рейки на крайних опорах. Поскольку на каждом участке изгиба прогибы рейки малы по сравнению с длиной, то кривизна рейки (линии ватерлинии) в каждой точке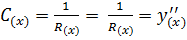   

Значение изгибающего момента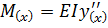

Для тонкой рейки можно принять 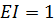. Тогда 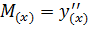. Это означает, что вторая производная от упругой линии рейки в каждой точке равна изгибающему моменту или кривизне в этой точке. При отсутствии в пролетах рейки внешней нагрузки и пренебрегая силами трения можно считать, что моменты вдоль пролетов изменяются линейно и тогда для любого сечения на участке i-1, i значение 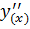можно записать как

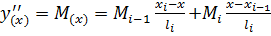
Дважды интегрируя это уравнение с учетом граничных условий, получим уравнение изгиба рейки на участке 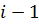,  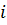–кубический сплайн.

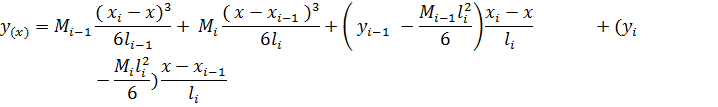
Количество таких уравнений равно количеству участков рейки.

Для получения окончательного решения уравнения изгиба рейки необходимо проверить плавность линий на соблюдение условий монотонности вторых производных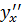

 >  > .… > > …. >

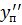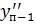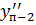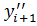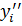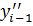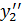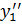
Сглаживание ватерлиний состоит в следующем:

-по начальным значениям полуширот 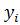, взятым из таблицы ординат, и заданным граничным условиям  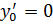и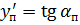

- решается система уравнений трех моментов и определяются все значения 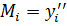     в первом приближении.

В том случае если некоторые 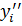   имеют знаки, обратные остальным 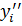, и не выполняется условие монотонности, то вносятся поправки в величины 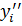, чтобы это условие выполнялось и знаки 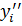были одинаковыми. Принимая новые сглаженные значения  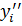и оставшиеся неизменными значения остальных 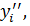вычисляются новые величины полуширот  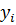из решения откорректированной системы уравнений трех моментов при неизменных значениях  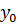и 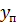 и известных значениях 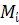. Полученные при решении новые значения полуширот  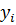cравнивают с исходными. Их отличие не должно превышать ранее установленного значения поправки ±ε_i .

Сглаживание шпангоутов и батоксов выполняется аналогично в диалоговом режиме на ЭВМ. При этом оценивается взаимное влияние поправок, вносимых в значение ординат, на гладкость всех кривых.

После сглаживания ватерлиний определяются окончательные значения 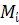 и составляются уравнения изгиба кривых для каждого участка ватерлиний, по которым определяются значения полуширот y_i.