Основы геометрической оптики. 6 страница

Упростим это выражение:

Очевидно, что под знаком натурального логарифма стоит геометрическая прогрессия, с параметрами ‑ . Сумма этой геометрической прогрессии равна ‑ 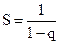. Поэтому выражение для средней энергии волны будет иметь вид:

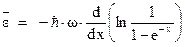
Преобразуем полученное выражение:

И теперь, в формулу Рэлея-Джинса нужно подставить именно это значение энергии, а не :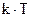

Или

                                   (2.8)

Это и есть формула Планка для теплового излучения тел. Она прекрасно согласуется с экспериментальными данными. Более того, используя формулу Планка можно получить теоретическое выражение для констант. В частности, постоянной Стефана-Больцмана. Использовав закон Стефана-Больцмана, получим:

Отсюда получаем теоретическое значение постоянной Стефана-Больцмана, которое очень хорошо согласуется с экспериментальными данными .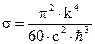

То же самое относительно постоянной Вина. Длина волны   соответствует максимуму излучения, т.е. максимуму функции Планка. Следовательно, взяв производную от функции Планка по длине волны, и приравняв ее к нулю, мы получим выражение для постоянной Вина:

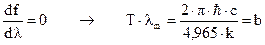
Подставив значения мировых констант, получим хорошее совпадение с экспериментом.

 

Оптическая пирометрия, дистанционный, бесконтактный метод измерения температуры.

Для дистанционного измерения температуры тел используют так называемый пирометр. Принципиальная схема пирометра изображена на рис. 2.4.

Здесь 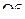   ‑ объектив,    ‑ окуляр,    ‑ спираль,    ‑ амперметр, градуированный в градусах Цельсия или Кельвина,    ‑ реостат, с помощью которого можно менять силу тока в цепи,    ‑ источник тока.

Исследователь наводит пирометр на светящийся объект (электрическая лампочка, пламя свечи, расплавленный металл в печи, Солнце, звезды и т.д.). С помощью окуляра добивается резкого изображения спирали на фоне объекта. Изменяя реостатом силу тока в цепи, изменяет степень накала спирали, добиваясь того, чтобы яркость спирали равнялась бы яркости объекта. При совмещении яркостей, по шкале амперметра, которая предварительно была проградуирована в градусах, определяют яркостную температуру объекта, т.е. температуру его поверхности.

С помощью специальных поправок можно вычислить термодинамическую температуру исследуемого тела.

 

 

Лекция 8 (2 часа)

 

Фотоэлектрический эффект. Эффект Комптона.  

(Фотоны, их основные характеристики. Внешний, внутренний, вентильный фотоэффект. Опыты Герца. Опыты Столетова. Основные законы фотоэффекта. Красная граница фотоэффекта. Элементарная теория фотоэффекта. Формула Эйнштейна. Задерживающий потенциал. Зависимость граничной частоты от величины задерживающего потенциала. Эффект Комптона и его теория. Давление света. Внешний фотоэффект . )

Фотоэлектрическим эффектом, или просто фотоэффектом, называется испускание электронов веществом под действием света.

Но это было установлено много позже, а в начале события развивались следующим образом.

В 1887 г Г.Герц заметил, что проскакивание искры между цинковыми шариками разрядника значительно облегчается, если один из шариков облучать ультрафиолетовым светом.

В 1889 – 1890 гг. это явление тщательно исследовал А.Г.Столетов. При этом оно установил следующее.

1. Под действием света вещество теряет только отрицательный заряд.

2. Наибольшее действие оказывают ультрафиолетовые лучи.

3. Величина испущенного телом заряда пропорциональна поглощенной им световой энергии.

4. Это явление практически безинерционно.

Третий пункт обычно носит название закона Столетова . Здесь 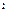   ‑ ток в цепи разрядника,    ‑ световой поток.

В 1898 г. Ленард и Томсон измерили удельный заряд отрицательных частиц, вырванных из цинка, по отклонению их в электрических и магнитных полях и установили, что ими являются электроны.

Явление вырывания электронов из металла под действием света наружу впоследствии получило название внешнего фотоэффекта.

Дальнейшее исследование фотоэффекта было связано с техническими усовершенствованиями.

Если в первых опытах Г.Герца между цинковыми шариками необходим был газ (для создания тока разряда за счет ионизации газа), то для самого фотоэффекта газ был не нужен и просто мешал (т.к. ток возникал за счет электронов, вырываемых из самого металла).

Поэтому анод и катод стали помещать в стеклянный баллон, в котором создавался глубокий вакуум. Но на само явление фотоэффекта продолжали еще оказывать мешающее влияние состояния поверхности излучающего электрода. Для устранения этого затруднения Миликен разработал способ очистки поверхности электрода находящегося в вакууме.

Теперь можно было проводить дальнейшее исследование фотоэффекта (см. рис. 2.5). Здесь большую роль сыграло исследование зависимости фототока от напряжения при постоянной освещенности, т.е. вольтамперная характеристика. Типичный вид вольтамперной характеристики приведен на рис. 2.6.

Даже при не очень большом анодном напряжении, порядка нескольких десятков вольт, фототок достигает насыщения ‑ . Т.е. все электроны, вырванные светом ускоряются полем и достигают анода.

Количество электронов зависит от светового потока, поэтому для разных световых потоков ток насыщения оказался разным.

Далее, оказалось, что фототок не равен нулю даже тогда, когда ускоряющая разность потенциалов была равна нулю. Следовательно, электроны, вылетая из металла, обладают некоторой начальной скоростью. И чтобы ток в цепи отсутствовал, необходимо приложить разность потенциалов обратной полярности, величины .

Таким образом, электрон, вылетая из металла с начальной скоростью , т.е. имея кинетическую энергию , тратит эту энергию движения на приобретение потенциальной энергии в поле ‑ . Если эти энергии равны, то электрон остановится у анода и полетит назад. При этом потенциальная энергия поля будет снова переходить в кинетическую энергию.

Следовательно, при условии:

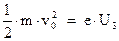
фототок будет равен нулю.

Дальнейшие усилия были направлены на исследование зависимости величины   от разных внешних условий.

Здесь необходимо упомянуть работы Лукирского и Прилежаева, которые сконструировали и изготовили сферический фотоэлемент, позволяющий очень точно регистрировать величину .

При исследованиях величины   было установлено следующее.

1.   от интенсивности света ( 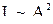) не зависит .

2.   в зависимости от частоты монохроматического света меняется по линейному закону:

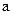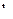где   и    ‑ константы, причем  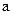не зависит от сорта металла, применявшегося для исследования фотоэффекта. График этого закона имеет вид, изображенный на рис. 2.7.

Из рисунка следует:

Отсюда вытекает, что существует минимальная частота, ниже которой фотоэффект не наблюдается. Если 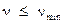, то    и 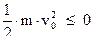, т.е. кинетическая энергия фотоэлектрона равна нулю.

Эта частота 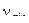   называется красной границей фотоэффекта.

Все эти опытные законы фотоэффекта противоречат волновым представлениям о свете.

1). Согласно волновой теории, энергия волны (интенсивность) зависит от квадрата амплитуды волны. Следовательно, кинетическая энергия вылетающих электронов должна зависеть от интенсивности падающего света (квадрата амплитуды), а не от частоты падающего света.

2). Также с волновой точки зрения не объяснимо существование красной границы фотоэффекта (какая бы не была интенсивность падающего света, а фотоэффект не наблюдается).

3). Также по-другому должен бы проходить сам фотоэффект. При малых интенсивностях электроны бы накапливали вначале энергию волны, а потом бы происходил процесс отрыва их от атома. В то время как на самом деле, фотоэффект практически безинерционное явление.

Т.е. результаты опытов противоречат классической теории. Для объяснения явления фотоэффекта Эйнштейн применил теорию Планка о квантовом характере излучения. Он предположил, что свет, световая энергия, также и поглощается порциями, квантами света. Причем эти порции-кванты в точности равны квантам энергии Планка:

Электрон получил квант энергии . Далее эта энергия частично расходуется на совершение работы выхода электрона из металла ‑ , либо , где    ‑ потенциал выхода. А если осталась еще энергия, то этот остаток будет являться начальной кинетической энергией электрона. Таким образом, Эйнштейн предложил формулу фотоэффекта:

                                   (2.9)

Т.о. гипотеза квантов сразу объяснила зависимость фотоэффекта от частоты падающего света.

Из формулы Эйнштейна следовало наличие красной границы фотоэффекта 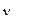, т.е. минимальной энергии кванта, хватающей только на совершение работы выхода:

Далее, если , то электрон, поглотив квант, сразу обладает энергией, достаточной для совершения работы выхода, и обладания начальной скоростью. Т.е. здесь находит объяснение безинерционность фотоэффекта.

Из формулы Эйнштейна вытекает эмпирическая формула для задерживающего напряжения . Действительно, из (2.9) вытекает:

Отсюда ‑ . Или 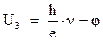. Следовательно,   и действительно не зависит от природы катода, а определяется универсальными константами. Кроме того, отсюда следует, что , т.е. эта константа равна потенциалу выхода для данного катода.

Таким образом, имея экспериментальный график зависимости   от 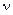, можно найти отношение постоянной Планка к заряду электрона ‑ 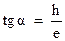. И, соответственно, зная заряд электрона рассчитать постоянную Планка.

 

Внутренний фотоэффект

В дальнейшем было открыто явление внутреннего фотоэффекта, о котором мы уже вкратце упоминали.

Это явление связано уже не с проводниками (металлами), а с полупроводниками. Как известно, полупроводники являются таковыми вследствие того, что все уровни валентной зоны уже заняты электронами, а для попадания на разрешенные уровни зоны проводимости необходимо преодолеть запрещенную зону (см. рис. 2.8). Для этого электроны должны обладать значительной энергией. Такой необходимой энергией обладают немногие электроны, поэтому полупроводники и довольно плохо проводят электрический ток.

Однако если полупроводник облучать светом, то электроны будут получать дополнительную энергию за счет квантов света и, если эта энергия достаточна, они будут попадать в зону проводимости. При этом в валентной зоне останутся дырки. Таким образом, проводимость полупроводника резко возрастает.

Аналогичным эффектом будут обладать, очевидно, и примесные полупроводники.

На этом свойстве полупроводников основано действие так называемых фотосопротивлений, фоторезисторов, величина сопротивления которых зависит от освещенности. На схемах фоторезисторы обозначаются так, как показано на рис. 2.9.

 

Вентильный фотоэффект

Рассмотрим теперь контакт полупроводников двух типов примесной проводимости.

Как известно, на этой границе раздела возникает запирающее напряжение. Это напряжение является запирающим для основных носителей тока, а для неосновных носителей оно, соответственно, будет ускоряющим.

Будем облучать теперь полупроводниковый контакт светом. При этом кристаллах будут возникать неосновные носители. Конечно, будут возникать и основные носители, но мы ими сейчас не интересуемся, поскольку они будут останавливаться запирающим напряжением. А неосновные носители будут проходить запирающий слой, и скапливаться на внешних границах.

Если теперь соединить эти границы проводником, то по цепи потечет ток. Величина этого тока зависит, очевидно, от энергии падающего света.

Такие устройства могут применяться для измерения освещенности, для создания так называемых солнечных батарей.

 

Корпускулярно-волновой дуализм

Итак, было показано, что свет излучается и поглощается порциями ‑ квантами. Носителями этой энергии являются особые световые частицы ‑ фотоны.

Рассмотрим характеристики фотона.

1). Фотон обладает энергией

                            (2.10)

2). Фотон обладает массой. Действительно, согласно теории относительности

              (2.11)

Однако мы знаем, что масса зависит от скорости: . Скорость фотона равна скорости света 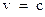. Отсюда вытекает, что . Однако, масса фотона не равна бесконечности . Отсюда мы вынуждены заключить, что масса покоя фотона равна нулю . В этом случае    ‑ неопределенность, может принимать любое значение.

Таким образом, фотон не может не двигаться и его скорость не может не равняться скорости света.

То, что фотон обладает гравитационной массой, убеждает нас отклонение лучей света, идущих от звезд, в гравитационном поле Солнца. Кроме того, так как гравитационная масса эквивалентна гравитационной массе, то фотон обладает и инертной массой.

3). Фотон обладает импульсом. Действительно, согласно теории относительности:

А так как для фотона 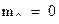, то

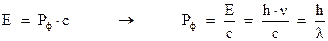              (2.12)

Но если фотон обладает импульсом, то он должен давить на преграду. Это было доказано точнейшими экспериментами русского физика Лебедева.

В то же время свет обладает волновыми свойствами (интерференция, дифракция, поляризация).

Как это сопоставить с нашими обычными представлениями о материи? Эти противоречивые свойства света представляют следующим образом.

Пусть в некоторой среде распространяется свет. Интенсивность света в некоторой точке этой среды определяется квадратом амплитуды волны ‑ . А энергия волны в некотором объеме , окружающем рассматриваемую точку, будет определяться как . 

С другой стороны, энергия в объеме  будет определяться плотностью потока фотонов. Поскольку реально энергию несут фотоны (ведь в обычном понимании энергия волны ‑ это энергия колеблющихся частиц среды, а среды для распространяющихся электромагнитных волн вообще не существует), то говорят, что волновые характеристики определяют вероятность нахождения фотона в той или иной области пространства, где мы их определяем.

Если    ‑ вероятность обнаружения фотона, то обычно записывают:

Отсюда    ‑ плотность вероятности обнаружения фотона, будет равна:

Т.е. волновые характеристики, волновые законы определяют вероятность нахождения фотона, или вероятность обнаружения фотона, прошедшему по пути, предписанному волновой теорией.

Обычно плотность потока фотонов очень велика и мы не замечаем этого вероятностного прохождения фотона.

Но это было показано экспериментально следующим образом.

Наблюдали интерференционную картину от двух когерентных источников света. Затем уменьшали интенсивность света, или плотность потока фотонов. При очень малых плотностях интерференционная картина начинала «мигать». Т.е. на экран, в область максимума, попадали то   фотонов, то   фотонов.   фотонов глаз наблюдателя видел, а    ‑ нет, так как порог зрения человека ‑   фотонов.

Но попадали фотоны именно в те места, в которые предписывали законы волновой оптики, т.е. в места максимумов. Там, где согласно волновой теории должны были быть минимумы освещенности ‑ всегда было темно. Там где области максимума, происходило мигание.

Когда на месте экрана поместили фотопластинку и произвели съемку интерференционной картины с длительной выдержкой, то фото не отличалось от фото с большими интенсивностями света.

Таким образом, мы приходим к представлениям о корпускулярно-волновом дуализме фотонов.

 Эффект Комптона.

 

Рассмотрим взаимодействие рентгеновского фотона со свободным электроном. Так энергия рентгеновского фотона очень велика, то рассмотрение необходимо вести с учетом релятивистских эффектов.

Пусть имеется первичный фотон , который налетает на покоящийся электрон   (см. рис. 3.10). После взаимодействия энергия первичного фотона изменится и у нас будет вторичный фотон , распространяющийся под углом   к направлению падающего фотона. Энергия электрона тоже изменится, и после взаимодействия у нас будет электрон отдачи , летящий под углом   к направлению падающего фотона.

При взаимодействии должен выполняться закон сохранения энергии ‑ энергия системы до взаимодействия должна равняться энергии системы после взаимодействия:

(I)

Здесь:    ‑ постоянная Планка, 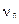   ‑ частота падающего фотона,    ‑ масса покоя электрона, 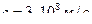   ‑ скорость света в вакууме,  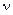  ‑ частота рассеянного фотона,    ‑ масса электрона отдачи, 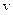   ‑ скорость электрона отдачи.

Далее, при взаимодействии также должен выполняться закон сохранения импульса:

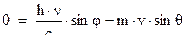(II)

(III)

Здесь:    ‑ импульс падающего фотона,    ‑ проекция импульса отраженного фотона на направление падающего фотона, 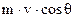   ‑ проекция импульса электрона отдачи на направление падающего фотона,    ‑ проекция импульса отраженного фотона на направление, перпендикулярное направлению падающего фотона,    ‑ проекция импульса электрона отдачи на направление, перпендикулярное направлению падающего фотона.

Из этих уравнений можно, задавшись например углом , найти три другие величины ‑ .

Из третьего уравнения выразим :

Обозначив, как обычно, , и учтя зависимость массы от скорости, выразим отсюда :

Таким образом, у нас осталась система двух уравнений:

Возведя второе уравнение в квадрат, перегруппировав члены, и разделив второе уравнение на первое, получим:

И это значение   подставим в первое уравнение системы, получим: