Основы геометрической оптики. 9 страница

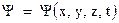
Рассмотрим простейший случай волновой функции, зависящей только от одной пространственной координаты 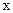   ‑   и простейший вид волновой функции ‑ плоскую, монохроматическую волну:

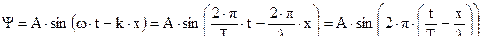
Окончательно волновую функцию запишем в виде:

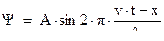                             (3.12)

где 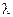   ‑ длина волны,  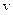  ‑ скорость ее распространения. Согласно гипотезе де-Бройля, .

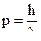Поскольку волна монохроматическая, то 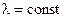, отсюда и импульс постоянен 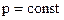. Т.е. импульс имеет строго определенное значение. Следовательно, изменение импульса ‑ интервал его возможных значений ‑ равен нулю. Значение импульса  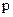 одно единственное и четко определено ‑ .

В то же время, рассматриваемая монохроматическая волна бесконечна, она не имеет ни начала, ни конца и заполняет все пространство 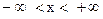. Следовательно, значение  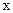 неопределенно и интервал возможных значений  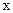  равен бесконечности. Итак

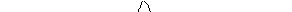Т.е. такой объект как плоская монохроматическая волна имеет совершенно определенный импульс и совершенно неопределенную область локализации.

Рассмотрим теперь другой объект ‑ волновой пакет (см. рис. 3.18). Т.е. такую волну, которая отлична от нуля лишь в некотором интервале 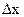, а во всех остальных точках пространства равна нулю.

Такой волновой пакет можно получить, складывая монохроматические волны разных частот, т.е. разных длин волн, в некотором интервале от 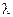  до 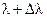. Следовательно, область локализации такого объекта уменьшилась и стала .

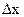Посмотрим теперь, что стало с импульсом. А импульс стал неопределенен. Ведь импульс определяется через длину волны 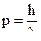, а волновой пакет состоит из целой серии волн, разной длины. Поэтому импульс потерял свое определенное значение. Интервал возможных значений импульса заключен в пределах:

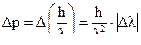
Чем более узкая область локализации пакета ‑ 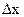, тем более широкий диапазон  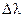 длин волн должен быть для его реализации. В пределе, очевидно, получим:

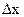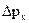Соотношение между   и   (аналогично и для других координат) впервые проанализировал Гейзенберг. Он исходил из следующего.

Чтобы определить положение и импульс электрона, его нужно осветить, т.е. получить от него хотя бы один рассеянный фотон. При этом, вследствие дифракции, точность в определении положения электрона не может быть больше длины волны фотона: 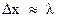. Чем точнее нужно измерить положение электрона, тем короче должна быть длина волны .

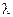Но при рассеянии фотона электрон получает отдачу и его импульс меняется на величину 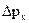  порядка импульса фотона 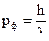, что и составит погрешность в определении импульса электрона 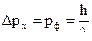. Следовательно, получим: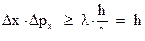

Это соотношение и носит название соотношение неопределенностей. Аналогичные соотношения имеют место и для других координат.

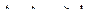
                           (3.13)

Таким образом, полученные соотношения связывают область локализации волнового пакета и область длин волн, для его реализации.

 

Электрон в электронно-лучевой трубке и в атоме

Итак, соотношение неопределенностей отражает корпускулярно-волновой дуализм материальных тел. С помощью этих соотношений, можно определить в каком случае, какими представлениями необходимо пользоваться.

Например, движение электрона в электронно-лучевой трубке.

Пусть неопределенность в определении импульса составляет 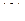, т.е.

Тогда неопределенность в определении его координаты будет равна

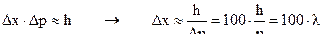
При скорости электрона  

В этом случае неопределенность локализации будет равна:

Т.е область локализации электрона ‑ 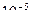  ‑ гораздо меньше размеров электронно-лучевой трубки  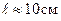 и здесь можно смело использовать корпускулярные представления об электроне.

В то же самое время для атома   использование корпускулярных представлений бессмысленно.

 

Длина волны де-Бройля покоящихся тел

Теперь можно рассмотреть вопрос об определении длины волны покоящегося тела, например электрона.

Формально мы получим:

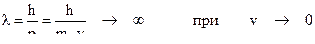
Но согласно соотношению неопределенности

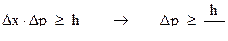
Подставив неопределенность импульса в определение длины волны, получим:

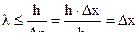
Таким образом, длину волны покоящейся частицы мо сможем определить с точностью до области локализации.

Для малых скоростей длина волны де-Бройля соответствует области локализации, а при больших скоростях она меньше области локализации.

Для макроскопических тел при малых скоростях:

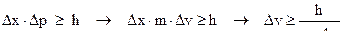
Следовательно, нельзя говорить, что скорость тела равна нулю. Нужно говорить, что тело обладает минимальной скоростью:

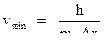
где 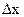   ‑ точность определения координаты тела. Таким образом, длина волны де-Бройля макроскопических тел

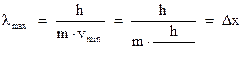
равна точности определения координаты тела.

 

Физический смысл волновой функции

Мы уже отмечали, что в квантовой механике частицы описываются с помощью волновой функции 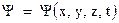. К истолкованию физического смысла  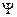 функции можно подойти, сравнивая ее с толкованием электромагнитной волны в вопросе дуализма фотона. В частности плотность энергии электромагнитной волны пропорциональна квадрату амплитуд напряженности электрического и магнитного полей.

Аналогично этому, произведение квадрата модуля волновой функции на элемент объема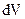

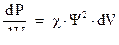                                   (3.14)

физически толкуется как вероятность того, что действие частицы будет обнаружено в объеме 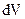. Т.е.  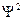 толкуется как плотность вероятности обнаружения частицы.

Функция 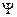  очевидно должна удовлетворять условию нормировки

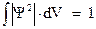
Т.е. вероятность обнаружения частицы где-нибудь в пространстве равна единице ‑ частица существует.

Следует иметь ввиду, что область действия (или что то же самое область обнаружения) не совпадает с областью локализации. Например, область действия ‑ захват электрона ионом, ограничена размерами иона. А область локализации электрона гораздо больше.

 

Волновая функция заряженной частицы

Поскольку функция 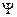  характеризует вероятность, то математический аппарат квантовой механики резко отличается от математического аппарата классической физики.

Предположим, что нам известна 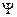-функция какой либо частицы. Как теперь найти параметры этой частицы? Координаты 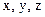. Импульс .

Эта задача в квантовой механике решается своеобразным приемом. Каждой величине ставится в соответствие свой оператор. Подействовав этим оператором на 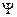-функцию находят искомый параметр.

Например.

Пусть частица двигается вдоль оси 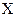  и пусть ее импульс определен точно. В этом случае, как мы уже видели, частице сопоставляется монохроматическая, плоская волна. Фаза этой монохроматической волны имеет вид:

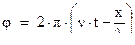
Используя соотношения 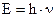  и 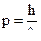, выражение для фазы волны перепишем в виде:

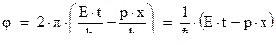
Волновая функция незаряженной частицы есть гармоническая функция sin или cos от 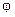. Если частица заряжена, то волновая функция комплексна:

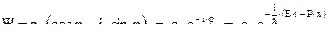               (3.15)

 

Операторы импульса и энергии

Продифференцируем 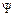-функцию по :

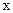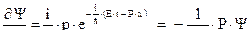
Или

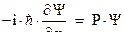
Таким образом, значение импульса мы получим как множитель перед 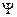-функцией, если применить к ней операцию ‑ 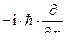. Эту операцию будем называть оператором импульса ‑ 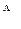. Таким образом

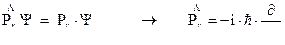
Аналогично можно получить и для других координат:

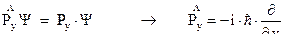
Найдем теперь выражение для оператора энергии из условия, что должно выполняться равенство 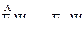. Для этого продифференцируем 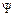-функцию по времени:

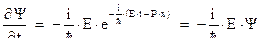
Отсюда 

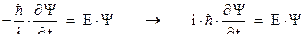
Т.е. оператор энергии имеет вид:

 

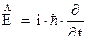
Уравнение Шредингера

С другой стороны, энергия частицы имеет вид: 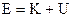, где    ‑ кинетическая энергия, 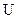   ‑ потенциальная энергия. Т.е.

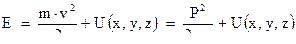
Квадрат импульса равен сумме квадратов проекций импульса, т.е.

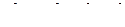
Представим теперь проекции импульсов в виде операторов:

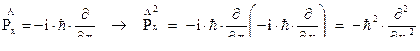
Т.е.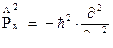                                      

Аналогично и по другим координатам:

Следовательно, оператор кинетической энергии будет иметь вид:

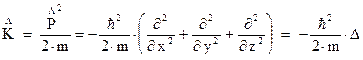
где 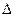   ‑ оператор Лапласа ‑ .

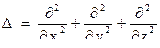Таким образом, оператор кинетической энергии будет иметь вид:

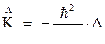
Потенциальная энергия содержит только координаты. Поэтому оператор 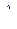  есть просто умножение на функцию .

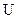Таким образом, оператор полной энергии, называемый оператором Гамильтона 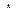, будет иметь вид:

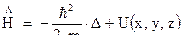
Таким образом, используя предыдущее выражение для оператора полной энергии, мы получим следующее уравнение:

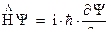                                      (3.16)

Это уравнение называется уравнением Шредингера. В раскрытом виде уравнение Шредингера имеет вид:

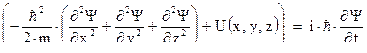         (3.17)

Уравнение Шредингера для стационарных состояний имеет вид:

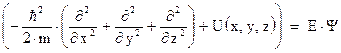            (3.18)

Специальными исследованиями было показано, что это уравнение при больших массах переходит в уравнение классической физики.

 

Пример

Рассмотрим заряженную частицу в бесконечно глубокой, одномерной потенциальной яме (см. рис. 3.19).

Поскольку случай одномерный и стационарный, то уравнение Шредингера будет иметь вид:

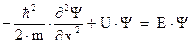
Вне потенциальной ямы 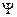-функция будет равна нулю.

Внутри потенциальной ямы 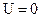, и поэтому для этой области пространства уравнение Шредингера будет иметь вид:

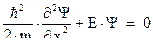
Граничные условия для функции 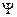  записываются как:

Преобразуем уравнение для :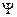

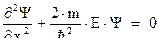
Введем обозначение:

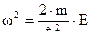
Окончательное дифференциальное уравнение для нахождения 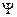-функции будет иметь вид:

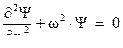
Как видим, получили дифференциальное уравнение незатухающих колебаний (I.2.4), только не во времени, а в пространстве. Решение этого уравнения имеет вид (I.2.6):

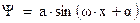
Константы интегрирования 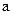  и 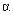  находятся из граничных условий.

1. Удовлетворим граничному условию в нуле ‑ 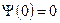. Получим ‑ 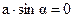. Отсюда вытекает, что константа интегрирования 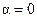. Таким образом, 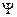-функция будет иметь вид ‑ .

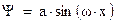2. Удовлетворим теперь второму граничному условию ‑ 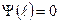. Получим ‑ 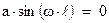. Отсюда вытекает, что должно выполняться услови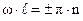е ‑ , где 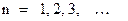Таким образом, для циклической частоты колебаний в пространстве получаем следующее выражение:

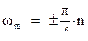
Следовательно, 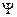-функции будет иметь вид:

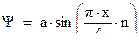
Выражение для амплитуды 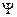-функции найдем из условия нормировки ‑ 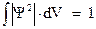. Для нашей задачи условие нормировки будет иметь вид:

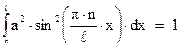
Возьмем интеграл этого уравнения:

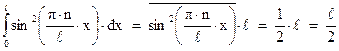
Следовательно, условие нормировки примет вид:

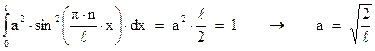
Окончательно 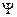-функцию представим в виде:

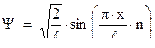
Графики самой 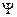-функции и  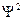  ‑ характеризующий вероятность нахождения частицы в том или ином месте потенциальной ямы, представлены на рис. 3.20.

 

Получим теперь выражение для энергии частицы в потенциальной яме.

Из выражения для квадрата частоты следует, что 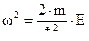. Из граничных условий вытекает, что 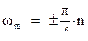. Объединяя эти два условия, получим:

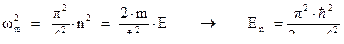
Мы видим, что энергия частицы квантуется, принимает дискретный ряд значений.

 

Лекция 12 (2 часа)

 

 Уравнение Шредингера.  

(Решение уравнения Шредингера для простейших одномерных задач. Частица в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Прохождение частицы сквозь потенциальный барьер. Гармонический осциллятор. Туннельный эффект.)

 

 

Рассмотрим заряженную частицу в бесконечно глубокой, одномерной потенциальной яме (см. рис. 3.19).

Поскольку случай одномерный и стационарный, то уравнение Шредингера будет иметь вид:

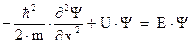
Вне потенциальной ямы 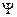-функция будет равна нулю.

Внутри потенциальной ямы 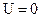, и поэтому для этой области пространства уравнение Шредингера будет иметь вид:

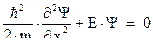
Граничные условия для функции 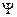  записываются как:

Преобразуем уравнение для :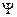

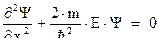
Введем обозначение:

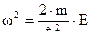
Окончательное дифференциальное уравнение для нахождения 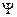-функции будет иметь вид:

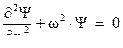
Как видим, получили дифференциальное уравнение незатухающих колебаний (I.2.4), только не во времени, а в пространстве. Решение этого уравнения имеет вид (I.2.6):

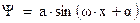
Константы интегрирования 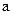  и 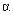  находятся из граничных условий.

1. Удовлетворим граничному условию в нуле ‑ 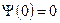. Получим ‑ 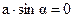. Отсюда вытекает, что константа интегрирования 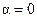. Таким образом, 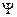-функция будет иметь вид ‑ .

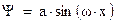2. Удовлетворим теперь второму граничному условию ‑ 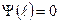. Получим ‑ 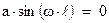. Отсюда вытекает, что должно выполняться услови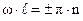е ‑ , где 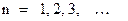Таким образом, для циклической частоты колебаний в пространстве получаем следующее выражение: