 |
Главная |
Теорема существования и единственности
|
из
5.00
|
Известно, какую большую роль в алгебре играют теоремы, отвечающие на вопрос о том, сколько решений имеет та или другая система алгебраических уравнении. В теории дифференциальных уравнений важным теоретическим вопросом является вопрос о том, насколько много решений имеет дифференциальное уравнение. Оказывается, что каждое дифференциальное уравнение имеет бесконечное множество решений, и потому приходится ставить вопрос не о числе решений, а о том, как можно описать совокупность всех решении данного дифференциального уравнения. Ответ на этот вопрос дает теорема существования и единственности (теорема 1), которая в этом параграфе приводится без доказательства. Доказательство будет дано значительно позже (см. §12).
Теорема 1. Пусть  - дифференциальное уравнение. Будем предполагать, что функция
- дифференциальное уравнение. Будем предполагать, что функция  задана на некотором открытом множестве Г плоскости Р переменных.
задана на некотором открытом множестве Г плоскости Р переменных.  . Относительно функции f будем предполагать, что она сама и ее частная производная
. Относительно функции f будем предполагать, что она сама и ее частная производная 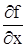 являются непрерывными функциями, на всем открытом множестве Г. Теорема утверждает
являются непрерывными функциями, на всем открытом множестве Г. Теорема утверждает
1) для всякой точки  множества Г найдется решение
множества Г найдется решение  уравнения (3), удовлетворяющее условию
уравнения (3), удовлетворяющее условию
 (4)
(4)
2) если два решения  и
и  уравнения (3) совпадают хотя бы для одного значения
уравнения (3) совпадают хотя бы для одного значения  , т. е. если
, т. е. если

то решения эти тождественно равны для всех тех значений переменного t, для которых они оба определены.
Числа  называют начальными значениями для решения
называют начальными значениями для решения 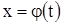 , а соотношение (4) — начальным условием для этого решения. Говорят также, что решение
, а соотношение (4) — начальным условием для этого решения. Говорят также, что решение 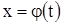 удовлетворяет начальному условию (4) или же что оно имеет начальные значения
удовлетворяет начальному условию (4) или же что оно имеет начальные значения  . Утверждение, что решение
. Утверждение, что решение  удовлетворяет начальному условию (4) (или имеет начальные значения
удовлетворяет начальному условию (4) (или имеет начальные значения  ), предполагает, что интервал
), предполагает, что интервал 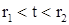 определения решения
определения решения  содержит точку
содержит точку  .
.
Таким образом, теорема 1 утверждает, что координаты любой точки  множества Г являются начальными значениями для некоторого решения уравнения (3) и что два решения с общими начальными значениями совпадают.
множества Г являются начальными значениями для некоторого решения уравнения (3) и что два решения с общими начальными значениями совпадают.
Геометрическое содержание теоремы 1 заключается в том, что через каждую точку  множества Г проходит одна и только одна интегральная кривая уравнения (3) (см. рис. 1).
множества Г проходит одна и только одна интегральная кривая уравнения (3) (см. рис. 1).
Говоря, что через каждую точку  множества Г проходит «только одна» интегральная кривая, мы допускаем некоторую неточность. В самом деле, решением уравнения (3) называется функция
множества Г проходит «только одна» интегральная кривая, мы допускаем некоторую неточность. В самом деле, решением уравнения (3) называется функция  , заданная на вполне определенном интервале
, заданная на вполне определенном интервале  . Наряду с этой функцией может существовать функция
. Наряду с этой функцией может существовать функция  , также удовлетворяющая уравнению (3) и имеющая те же начальные значения
, также удовлетворяющая уравнению (3) и имеющая те же начальные значения  , но заданная на другом интервале
, но заданная на другом интервале  . Вторая часть теоремы 1 утверждает лишь, что функции
. Вторая часть теоремы 1 утверждает лишь, что функции 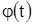 и
и  совпадают там, где они обе определены, но вовсе на утверждает, что интервалы их определения
совпадают там, где они обе определены, но вовсе на утверждает, что интервалы их определения  и
и  одинаковы.
одинаковы.

Если один из интервалов, например  , полностью содержит другой, то мы будем говорить, что решение
, полностью содержит другой, то мы будем говорить, что решение  , заданное на интервале
, заданное на интервале  является продолжением решения
является продолжением решения  . Естественно сосредоточить все внимание на тех решениях, которые нельзя продолжить ни вправо, ни влево. Такие решения мы будем называть непродолжаемыми. Нетрудно доказать, что каждое решение может быть продолжено до непродолжаемого и притом единственным способом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение том, что через каждую точку
. Естественно сосредоточить все внимание на тех решениях, которые нельзя продолжить ни вправо, ни влево. Такие решения мы будем называть непродолжаемыми. Нетрудно доказать, что каждое решение может быть продолжено до непродолжаемого и притом единственным способом. Если теперь подразумевать под интегральной кривой график непродолжаемого решения, то утверждение том, что через каждую точку  проходит единственная интегральная кривая, становится точным.
проходит единственная интегральная кривая, становится точным.
Каждое решение  уравнения (3) мы интерпретировали геометрически в виде графика функции
уравнения (3) мы интерпретировали геометрически в виде графика функции 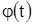 . Дадим теперь геометрическую интерпретацию самого уравнения (3). Через каждую точку
. Дадим теперь геометрическую интерпретацию самого уравнения (3). Через каждую точку  множества Г проведем прямую
множества Г проведем прямую  с угловым коэффициентом
с угловым коэффициентом 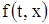 . Мы получаем поле направлений, соответствующее уравнению (3), что и дает геометрическую интерпретацию этого уравнения.
. Мы получаем поле направлений, соответствующее уравнению (3), что и дает геометрическую интерпретацию этого уравнения.
Связь между геометрической интерпретацией уравнения и геометрической интерпретацией его решений заключается в том (рис. 2), что любая интегральная кривая  в каждой своей точке
в каждой своей точке  касается прямой
касается прямой 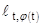 .
.
Примеры:
1. Для того чтобы проиллюстрировать значение теоремы 1 (в данном случае второй ее части), решим дифференциальное уравнение
 (5)
(5)
где  - действительное число. Здесь
- действительное число. Здесь

так что функция  в действительности зависит лишь от переменного х. Множество точек, на котором определена функция
в действительности зависит лишь от переменного х. Множество точек, на котором определена функция  , в данном случае совпадает со всей плоскостью Р. Как сама функция
, в данном случае совпадает со всей плоскостью Р. Как сама функция  , так и ее производная
, так и ее производная  являются непрерывными функциями переменных t и x во всей плоскости Р. Таким образом, теорема 1 к уравнению (5) применима. Непосредственной подстановкой в уравнение (5) проверяется, что каждая функция
являются непрерывными функциями переменных t и x во всей плоскости Р. Таким образом, теорема 1 к уравнению (5) применима. Непосредственной подстановкой в уравнение (5) проверяется, что каждая функция
 , (6)
, (6)
где с — произвольное действительное число, является решением уравнения (5). Решение это непродолжаемо, так как оно задано уже на всей прямой  . Покажем, что, придавая всевозможные значения числу с, мы получим все решения уравнении (5). Пусть
. Покажем, что, придавая всевозможные значения числу с, мы получим все решения уравнении (5). Пусть  - произвольное решение этого уравнения. Покажем, что при надлежащем выборе числа с мы имеем
- произвольное решение этого уравнения. Покажем, что при надлежащем выборе числа с мы имеем  . Пусть
. Пусть  - некоторая точка интервала существования решения
- некоторая точка интервала существования решения 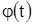 и
и  . Положим
. Положим  . Тогда решения
. Тогда решения  и
и  уравнения (5) имеют одинаковые начальные значения
уравнения (5) имеют одинаковые начальные значения  и потому в силу второй части теоремы 1 совпадают. Таким образом, формула (6) исчерпывает совокупность всех решений дифференциального уравнения (5).
и потому в силу второй части теоремы 1 совпадают. Таким образом, формула (6) исчерпывает совокупность всех решений дифференциального уравнения (5).
|
из
5.00
|
Обсуждение в статье: Теорема существования и единственности |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

