ГЛАВА IV . ПРАКТИЧЕСКИЯ СХЕМА РЕШЕНИЯ СИСТЕМЫ ДИФФЕРЕНЦАЛЬНЫХ УРАВНЕНИЙ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ

 

Найти общее решение системы дифференциальных уравнений.

 

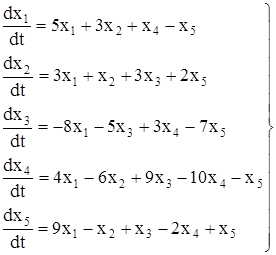                         (1)

 

Решение. Будем искать частное решение системы в следующем виде:

 

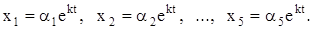                          (2)

 

Требуется определить постоянные 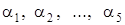 и k так, чтобы функции  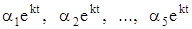удовлетворяли системе уравнений (1). Подставляя их в систему (1), получим

 

,

,

,

.

 

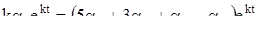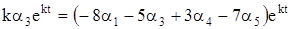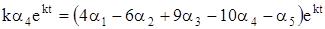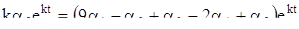Сократим на 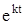. Перенося все члены в одну сторону и собирая коэффициенты при 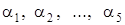, получим систему уравнений

 

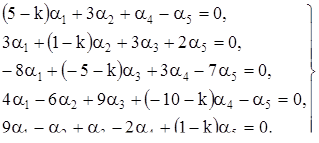                         (3)

 

Выберем 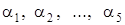 и k такими чтобы удовлетворялась система (3). Эта система есть система линейных однородных алгебраических уравнений относительно 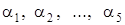. Составим определитель системы (3):

 

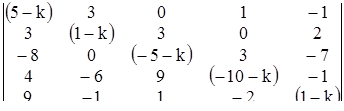                     (4)

 

Нетривиальные решения (2) мы получим только при таких k , при которых определитель (4) обращается в ноль. Мы приходим к уравнению пятого порядка для определения k:

 

,

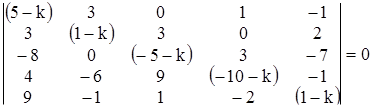или

 

.

 

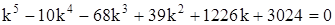Находим корни этого уравнения, используя математическую программу Mach Cad

 

 

Для каждого корня 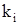(i=1, 2, 3, 4, 5) напишем систему (3) и определим коэффициенты 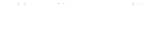. Можно показать, что один из них произвольный, его можно считать равным единице.

Для корня 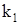 составим систему (3):

 

 

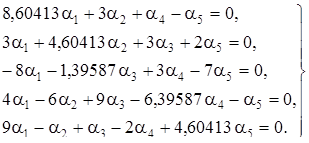
Пусть 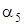=1, тогда получаем систему:

 

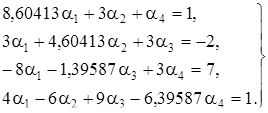
Решим эту систему с помощью программы реализующей метод Гаусса (см. приложение.)

Программа решения систем линейных уравнений по методу Гаусса

Введите порядок матрицы системы (max. 10)

> 4

Введите расширенную матрицу системы

 

A 1 2 3 4 b

 

1 8.6 3   0 1 1

2 3 4.6 3 0 -2

3 -8 0 -1.4 3 7

4 4 -6 9 -6.4 1

 

Результат вычислений по методу Гаусса

 

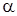1 = 2.4834281139E-01

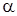2 = -1.6215428632E+00

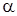3 = 1.5713562455E+00

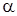4 = 3.7288804116E+00

 

Таким образом, используя формулу (2) получаем для корня 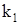 решение системы (1):

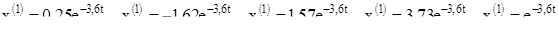
Для корня 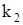 составим систему (3):

 

 

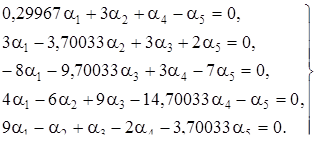
Пусть 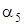=1, тогда получаем систему:

 

 

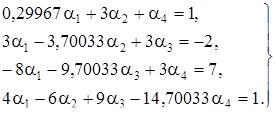
Решим эту систему с помощью программы реализующей метод Гаусса (см. приложение.)

 

Программа решения систем линейных уравнений по методу Гаусса

Введите порядок матрицы системы (max. 10)

> 4

Введите расширенную матрицу системы

 

A 1 2 3 4 b

 

1 0.3 3   0 1 1

2 3 -3.7 3 0 -2

3 -8 0 -9.7 3 7

4 4 -6 9 -14.7 1

Результат вычислений по методу Гаусса

 

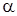1 = 1.2357323071E+01

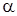2 = 5.8924432138E-01

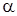3 = -1.2297255075E+01

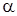4 = -4.4749298856E+00

 

Таким образом, используя формулу (2) получаем для корня 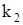 решение системы (1):

 

 

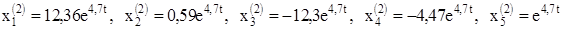
Для корня 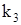 составим систему (3):

 

 

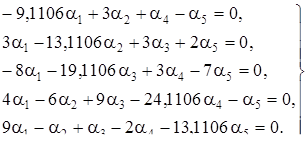
Пусть 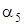=1, тогда получаем систему:

 

 

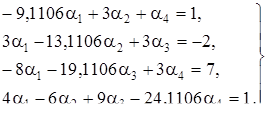
Решим эту систему с помощью программы реализующей метод Гаусса (см. приложение.)

Программа решения систем линейных уравнений по методу Гаусса

Введите порядок матрицы системы (max. 10)

> 4

Введите расширенную матрицу системы

 

A 1 2 3 4 b

 

1 -9.1 3  0 1 1

2 3 -13.1 3 0 -2

3 -8 0 -19.1 3 7

4 4 -6 9 -24.1 1

 

Результат вычислений по методу Гаусса

 

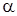1 = -1.1863988144E-01

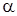2 = 4.5529392393E-02

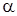3 = -3.5073275152E-01

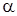4 = -2.0434711016E-01

 

Таким образом, используя формулу (2) получаем для корня 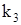 решение системы (1):

 

 

Для корня 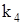 составим систему (3):

 

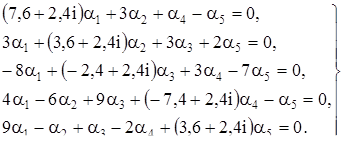
Пусть 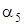=1, тогда получаем систему:

 

 

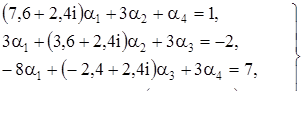
Решив эту систему методом Гаусса, получим:

 

 

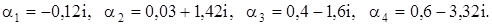
Таким образом, используя формулу (2) получаем для корня 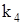 решение системы (1):

 

 

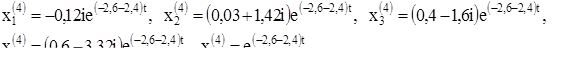
Для корня 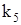 составим систему (3):

 

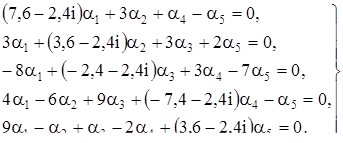
Пусть 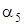=1, тогда получаем систему:

 

 

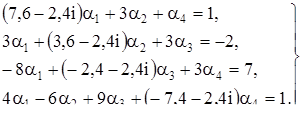
Решив эту систему методом Гаусса, получим:

 

 

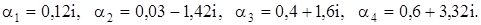
Таким образом, используя формулу (2) получаем для корня 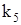 решение системы (1):

 

 

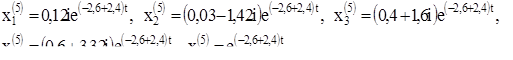
Выпишем комплексное решение

 

 

 

 

 

 

 

 

 

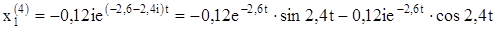
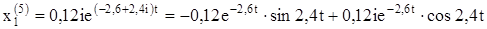
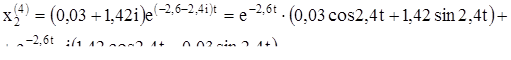
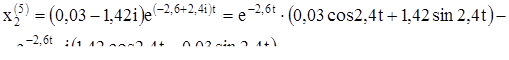
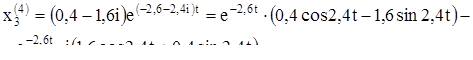
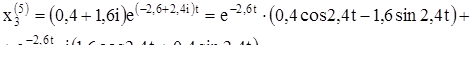
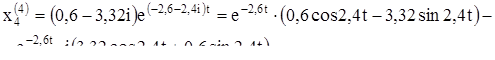
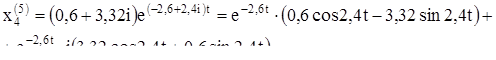
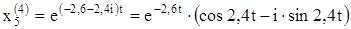
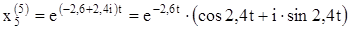
Решением будут действительные и мнимые части:

 

 

 

 

 

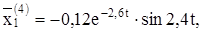
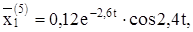
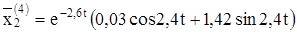
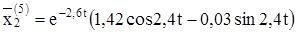
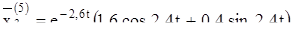
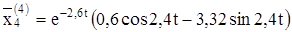
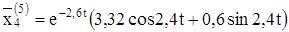
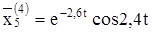
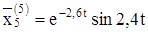
Теперь можем написать общее решение

 

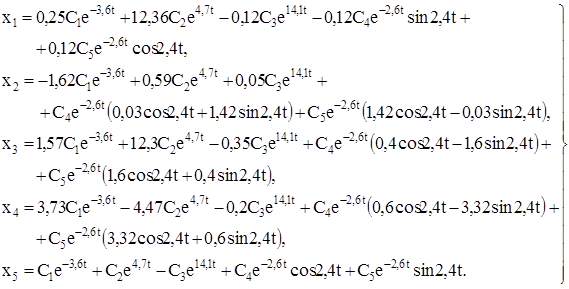
Исследуем устойчивость решения системы (1). Корни характеристического уравнения

 

 

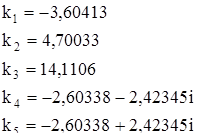
Для того, чтобы решение было устойчивым необходимо чтобы все действительные части корней характеристического уравнения были отрицательными. В данном случае 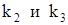 положительные. Отсюда делаем вывод, что решение системы (1) неустойчиво.

ЗАКЛЮЧЕНИЕ

В ходе исследовательской работы были рассмотрены линейные однородные и неоднородные уравнения с постоянными коэффициентами, системы линейных однородных дифференциальных уравнений с постоянными коэффициентами и один из методов их решения – метод исключения. Также были рассмотрены автономные системы дифференциальных уравнений и их фазовые пространства. Было проведено исследование фазовой плоскости линейных систем второго порядка. В работе приведены доказательства теорем существования и единственности как для одного уравнения, так и для нормальной системы уравнений. В ходе исследовательской работы было рассмотрено лишь понятие об устойчивости решений, не были рассмотрены важнейшие теоремы устойчивости, что является темой для дальнейшего исследования. В каждом параграфе приведены примеры, что значительно облегчает понимание темы.

Характерным для данной работы является то, что многие важные утверждения и их доказательства приведены в виде предложений или примеров, обозначенных А), Б), и т.д. Поэтому при изучении некоторых тем игнорирование этих примеров нежелательно, так как они используются при доказательстве основных теорем.

В практической части работы было найдено общее решение системы дифференциальных уравнений

 

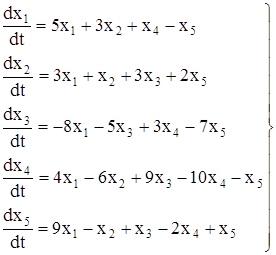
При решении этой системы была использована программа Mach Cad, составлена программа реализующая метод Гаусса на языке программирования Паскаль. При исследовании решения системы было выяснено, что решение системы не устойчиво.

ЛИТЕРАТУРА

 

1. Видаль П. Нелинейные импульсные системы: Монография: Пер. с фр. – М.: энергия, 1994. – 336с.

2. Гукасов Н.А. Механика жидкости и газа: Учеб. пособие для вузов. – М.: 1996. – 443с.

3. Камке Э. Справочник по обыкновенным дифференциальным уравнениям: – 5-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1976. – 576с.

4. Мудров А.Е.Численные методы для ПЭВМ на языках Паскаль, Фортран и Бейсик. МП “Раско”, Томск, 1991 г.

5. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов, т.2: Учеб. пособие для втузов. – 13-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1985. – 560 с.

6. Понтрягин Л.С. Обыкновенные дифференциальные уравнения: – 4-е изд. – М.: Наука, Главная редакция физико-математической литературы, 1974. – 332с.

7. Турчак Л. И. Основы численных методов: Учеб. пособие. – М.: Наука. Гл. ред. физ.-мат. лит, 1987.

8. Численные методы: Учеб. пособие для студентов физ.-мат. спец. пед. ин-тов/ Под ред. В. М. Заварыкин, В. Г. Житомирский, М. П. Лапчик. – М.: Просвещение, 1990.

ПРИЛОЖЕНИЕ

 

Описание алгоритма. В данной программе реализован метод Гаусса со схемой частичного выбора.

В переменную n вводится порядок матрицы системы. С помощью вспомогательной процедуры ReadSystem в двумерный массив a и одномерный массив b вводится c клавиатуры расширенная матрица системы, после чего оба массива и переменная n передаются функции Gauss. В фукции Gauss для каждого k-го шага вычислений выполняется поиск максимального элемента в k-м столбце матрицы начинаяя с k-й строки. Номер строки, содержащей максимальный элемент сохраняеется в переменной l. В том случае если максимальный элемент находится не в k-й строке, строки с номерами k и l меняются местами. Если же все эти элементы равны нулю, то происходит прекращение выполнения функции Gauss c результатом false. После выбора строки выполняется преобразование матрицы по методу Гаусса. Далее вычисляется решение системы и помещается в массив x. Полученное решение выводится на экран при помощи вспомогательной процедуры WriteX.

Листинг программы

Uses CRT;

 

Const

 maxn = 10;

 

Type

 Data = Real;

 Matrix = Array[1..maxn, 1..maxn] of Data;

 Vector = Array[1..maxn] of Data;

{ Процедура ввода расширенной матрицы системы }

Procedure ReadSystem(n: Integer; var a: Matrix; var b: Vector);

Var

 i, j, r: Integer;

Begin

 r := WhereY;

 GotoXY(2, r);

 Write('A');

 For i := 1 to n do begin

 GotoXY(i*6+2, r);

 Write(i);

 GotoXY(1, r+i+1);

 Write(i:2);

 end;

 GotoXY((n+1)*6+2, r);

 Write('b');

 For i := 1 to n do begin

 For j := 1 to n do begin

 GotoXY(j * 6 + 2, r + i + 1);

 Read(a[i, j]);

 end;

 GotoXY((n + 1) * 6 + 2, r + i + 1);

 Read(b[i]);

 end;

End;

 

{ Процедура вывода результатов }

Procedure WriteX(n :Integer; x: Vector);

Var

 i: Integer;

Begin

 For i := 1 to n do

 Writeln('x', i, ' = ', x[i]);

End;

 

 

{ Функция, реализующая метод Гаусса }

Function Gauss(n: Integer; a: Matrix; b: Vector; var x:Vector): Boolean;

Var

 i, j, k, l: Integer;

 q, m, t: Data;

Begin

 

 For k := 1 to n - 1 do begin

 

 { Ищем строку l с максимальным элементом в k-ом столбце}

 l := 0;

 m := 0;

 For i := k to n do

 If Abs(a[i, k]) > m then begin

 m := Abs(a[i, k]);

 l := i;

 end;

 

 { Если у всех строк от k до n элемент в k-м столбце нулевой,

 то система не имеет однозначного решения }

 If l = 0 then begin

 Gauss := false;

 Exit;

 end;

{ Меняем местом l-ую строку с k-ой }

 If l <> k then begin

 For j := 1 to n do begin

 t := a[k, j];

 a[k, j] := a[l, j];

 a[l, j] := t;

 end;

 t := b[k];

 b[k] := b[l];

 b[l] := t;

 end;

 

 { Преобразуем матрицу }

 For i := k + 1 to n do begin

 q := a[i, k] / a[k, k];

 For j := 1 to n do

 If j = k then

 a[i, j] := 0

 else

 a[i, j] := a[i, j] - q * a[k, j];

 b[i] := b[i] - q * b[k];

 end;

 

 end;

 

 { Вычисляем решение }

 x[n] := b[n] / a[n, n];

 For i := n - 1 downto 1 do begin

 t := 0;

 For j := 1 to n-i do

 t := t + a[i, i + j] * x[i + j];

 x[i] := (1 / a[i, i]) * (b[i] - t);

 end;

 

 Gauss := true;

End;

 

Var

 n, i: Integer;

 a: Matrix ;

 b, x: Vector;

Begin

 ClrScr;

 Writeln('Программа решения систем линейных уравнений по методу Гаусса');

 Writeln;

 

 Writeln('Введите порядок матрицы системы (макс. 10)');

 Repeat

 Write('>');

 Read(n);

 Until (n > 0) and (n <= maxn);

 Writeln;

 

 Writeln('Введите расширенную матрицу системы');

 ReadSystem(n, a, b);

 Writeln;

 

 If Gauss(n, a, b, x) then begin

 Writeln('Результат вычислений по методу Гаусса');

WriteX(n, x);

 end

 else

 Writeln('Данную систему невозможно решить по методу Гаусса');

 Writeln;

End.