 |
Главная |
Линейное неоднородное уравнение с постоянными коэффициентами
|
из
5.00
|
Здесь будет дано решение линейного уравнения с постоянными коэффициентами со свободным членом специального вида, являющимся так называемым квазимногочленом.
А) Квазимногочленом будем называть всякую функцию F(t), которую можно записать в виде:
 (1)
(1)
где  суть некоторые комплексные числа, а
суть некоторые комплексные числа, а  — многочлены от t. Из предложения А) § 6 следует, что каждое решение линейного однородного уравнения с постоянными коэффициентами является квазимногочленом. Можно доказать, что и обратно, каждый квазимногочлен является решением некоторою линейного однородного уравнения с постоянными коэффициентами. Если какие-нибудь два числа последовательности
— многочлены от t. Из предложения А) § 6 следует, что каждое решение линейного однородного уравнения с постоянными коэффициентами является квазимногочленом. Можно доказать, что и обратно, каждый квазимногочлен является решением некоторою линейного однородного уравнения с постоянными коэффициентами. Если какие-нибудь два числа последовательности  совпадают между собой, например, если
совпадают между собой, например, если  , то члены суммы (1), соответствующие этим числам, можно объединить и заменить членом
, то члены суммы (1), соответствующие этим числам, можно объединить и заменить членом  . Таким образом, запись (1) всегда можно привести к такому виду, что числа
. Таким образом, запись (1) всегда можно привести к такому виду, что числа  , входящие в нее, попарно различны. Отметим, что сумма и произведение двух произвольных квазимногочленов также есть квазимногочлен; далее, если к произвольному квазимногочлену применить произвольный оператор L(p), то мы вновь получим квазимногочлен.
, входящие в нее, попарно различны. Отметим, что сумма и произведение двух произвольных квазимногочленов также есть квазимногочлен; далее, если к произвольному квазимногочлену применить произвольный оператор L(p), то мы вновь получим квазимногочлен.
Таким образом, в настоящем параграфе будет рассматриваться уравнение
 (2)
(2)
где F(t) есть некоторый квазимногочлен. Наряду с уравнением (2) рассмотрим соответствующее однородное уравнение
 (3)
(3)
Нижеследующее предложение непосредственно вытекает из замечания Б) § 4.
Б) Если 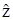 есть некоторое решенме уравнения (2), то произвольное z того же уравнения может быть записано в виде:
есть некоторое решенме уравнения (2), то произвольное z того же уравнения может быть записано в виде:

где u есть некоторое решение уравнения (3).
Так как произвольное решение однородного уравнения мы отыскивать уже умеем, то дело сводится, таким образом, к отысканию одного решения или, как говорят, частного решения уравнения (2) в случае, когда F(t) есть квазимногочлен. Так как, далее, каждый квазимногочлен записывается в виде (1), то в силу замечания В) § 4 дело сводится к отысканию частного решения уравнения (2) в случае, когда  где f(t) - многочлен. Для этого случая решение отыскивается в нижеследующей теореме.
где f(t) - многочлен. Для этого случая решение отыскивается в нижеследующей теореме.
Во избежание недоразумений отметим, что в дальнейшем под многочленом степени r мы будем понимать функцию вида  , не предполагая непременно, что старший коэффициент
, не предполагая непременно, что старший коэффициент  отличен от нуля.
отличен от нуля.
Теорема 6. Рассмотрим неоднородное уравнение
 (4)
(4)
в котором f(t) есть многочлен степени r относительно t, а  - комплексное число. Пусть k = 0, если
- комплексное число. Пусть k = 0, если  . Оказывается, что существует частное решение уравнения (4), имеющее вид:
. Оказывается, что существует частное решение уравнения (4), имеющее вид:
 (5)
(5)
где g(t) есть многочлен степени r относительно t. Коэффициенты многочлена g(t) можно найти методом неопределенных коэффициентов.
§ 8. Метод исключения
До сих пор мы занимались решением одного линейного уравнения с постоянными коэффициентами. Оказывается, однако, что весьма общую систему линейных уравнений с постоянными коэффициентами можно в некотором смысле свести к одному уравнению. Сведение это осуществляется методом исключения, аналогичным тому, который употребляется в теории линейных алгебраических (не дифференциальных) уравнений. Здесь будет дано изложение этого метода и сделаны некоторые выводы из него.
Мы будем рассматривать систему уравнений
 (1)
(1)
здесь 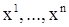 - неизвестные функции независимого переменного t, а
- неизвестные функции независимого переменного t, а  — заданные функции времени t. Каждый символ
— заданные функции времени t. Каждый символ  представляет собой многочлен с постоянными коэффициентами относительно оператора дифференцирования р, так что один член
представляет собой многочлен с постоянными коэффициентами относительно оператора дифференцирования р, так что один член 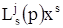 представляет собой линейную комбинацию с постоянными коэффициентами относительно функции
представляет собой линейную комбинацию с постоянными коэффициентами относительно функции  и ее производных. Число уравнений системы (1) равно числу неизвестных функции.
и ее производных. Число уравнений системы (1) равно числу неизвестных функции.
Порядок системы (1) относительно неизвестной функции  обозначим через
обозначим через  , так что общий порядок системы (1) определяется формулой
, так что общий порядок системы (1) определяется формулой  . Ставя задачу решения системы (1), мы, естественно, должны предполагать, что каждая неизвестная функция
. Ставя задачу решения системы (1), мы, естественно, должны предполагать, что каждая неизвестная функция  имеет все производные до порядка
имеет все производные до порядка  включительно; предположение о существовании производных более высоких порядков не вытекает из постановки задачи.
включительно; предположение о существовании производных более высоких порядков не вытекает из постановки задачи.
Применяя к системе (1) метод исключения, мы будем предполагать, что каждая из неизвестных функций  имеет достаточное число производных, точно так же, как и каждая из функций
имеет достаточное число производных, точно так же, как и каждая из функций  . Делая эти допущения, мы, с одной стороны, сужаем класс рассматриваемых решений (предположение о достаточной дифференцируемости неизвестных функций), а, с другой стороны, сужаем класс рассматриваемых уравнений (предположение о достаточной дифференцируемости функций
. Делая эти допущения, мы, с одной стороны, сужаем класс рассматриваемых решений (предположение о достаточной дифференцируемости неизвестных функций), а, с другой стороны, сужаем класс рассматриваемых уравнений (предположение о достаточной дифференцируемости функций 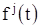 ). Первое из этих ограничений можно снять, доказав, что если
). Первое из этих ограничений можно снять, доказав, что если 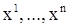 есть решение системы (1) и если правые части
есть решение системы (1) и если правые части  имеют достаточное число производных, то каждая из функций
имеют достаточное число производных, то каждая из функций  имеет достаточное число производных (см. примеры 3 и 4).
имеет достаточное число производных (см. примеры 3 и 4).
Перейдем к изложению метода исключения.
А) Рассмотрим матрицу
 (2)
(2)
системы уравнений (1). Каждый элемент  матрицы (2) есть многочлен относительно р. Таким образом, можно вычислить детерминант D(р) матрицы (2) и ее миноры. Алгебраическое дополнение элемента
матрицы (2) есть многочлен относительно р. Таким образом, можно вычислить детерминант D(р) матрицы (2) и ее миноры. Алгебраическое дополнение элемента  матрицы (2) (т. е. минор этого элемента, взятый с надлежащим знаком) обозначим через
матрицы (2) (т. е. минор этого элемента, взятый с надлежащим знаком) обозначим через  . Из курса высшей алгебры известно, что имеет место тождество:
. Из курса высшей алгебры известно, что имеет место тождество:
 (3)
(3)
где  есть так называемый символ Кронекера:
есть так называемый символ Кронекера:

Умножая уравнение (1) на многочлен  (т.е. производя ряд дифференцирований, умножений на числа и сложений) и суммируя затем по j, мы получаем равенство
(т.е. производя ряд дифференцирований, умножений на числа и сложений) и суммируя затем по j, мы получаем равенство
 (4)
(4)
(При переходе от равенств (1) к равенству (4) мы использовали существование достаточно большого числа производных у функций  и
и  .) В силу (3) равенство (4) можно переписать в виде
.) В силу (3) равенство (4) можно переписать в виде
 (5)
(5)
Полученная нами система уравнений (5) (  ) обладает тем свойством, что каждая неизвестная функция
) обладает тем свойством, что каждая неизвестная функция  входит лишь в одно уравнение (5). Мы доказали, таким образом, что если система функций
входит лишь в одно уравнение (5). Мы доказали, таким образом, что если система функций 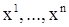 представляет собой решение системы (1), то каждая отдельная функция
представляет собой решение системы (1), то каждая отдельная функция  является решением уравнения (5).
является решением уравнения (5).
Не следует думать, однако, что если для каждого номера i выбрать произвольным образом решение  уравнения (5) и затем составить систему функций
уравнения (5) и затем составить систему функций 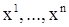 , то полученная система функций будет решением системы (1). Для того чтобы найти общее решение
, то полученная система функций будет решением системы (1). Для того чтобы найти общее решение 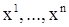 системы (1), нужно найти общее решение
системы (1), нужно найти общее решение  каждого уравнения (5),
каждого уравнения (5), 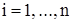 , составить систему функций
, составить систему функций  и затем выяснить, при каких условиях (при каких соотношениях между постоянными интегрирования) эта система функций удовлетворяет системе уравнений (1).
и затем выяснить, при каких условиях (при каких соотношениях между постоянными интегрирования) эта система функций удовлетворяет системе уравнений (1).
Сделаем теперь некоторые выводы из метода исключения. Формулируем прежде всего результат, полученный в предложении А), для случая однородной системы уравнений
 (6)
(6)
Б) Если система функций  представляет собой решение системы (6), то каждая отдельная функция
представляет собой решение системы (6), то каждая отдельная функция  , входящая в это решение, удовлетворяет уравнению
, входящая в это решение, удовлетворяет уравнению

где D(p) — детерминант матрицы  системы (6).
системы (6).
Покажем теперь, как, пользуясь методом исключения, следует решать, однородную систему уравнений (6).
Систему (6) перепишем в векторной форме
 (7)
(7)
где  - матрица системы (6), а
- матрица системы (6), а  .
.
В) Допустим, что детерминант D(p) системы (6) не обращается тождественно в нуль, и пусть  — корень многочлена D(p), имеющий кратность k. Будем искать решение уравнения (8), имеющее вид:
— корень многочлена D(p), имеющий кратность k. Будем искать решение уравнения (8), имеющее вид:
 (8)
(8)
г7де 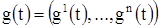 — вектор, компоненты
— вектор, компоненты
 (9)
(9)
которого являются многочленами степени k - 1 относительно t с неопределенными коэффициентами. Каждое решение вида (8) уравнения (7) мы будем называть соответствующим корню  .
.
Подставляя предполагаемое решение (8) в уравнение (7), мы получим:

После сокращения на  это дает:
это дает:
 (10)
(10)
Таким образом, вектор (8) тогда и только тогда является решением уравнения (8), когда многочлены (9) удовлетворяют условию (10). Переписывая векторное уравнение (10) в координатной форме, получим n соотношений:
 (11)
(11)
Левая часть каждого соотношения (11) представляет собой многочлен степени k - 1 относительно t, коэффициенты которого являются линейными однородными функциями коэффициентов многочленов (9). Приравнивая нулю коэффициент при каждой степени t в каждом из соотношений (11), мы получим систему линейных однородных уравнений относительно коэффициентов многочленов (9). Эта система эквивалентна уравнению (10).
Таким образом, изложенный метод сводит задачу отыскания решений вида (8) к решению некоторой линейной однородной системы алгебраических уравнений. Из сказанного видно, что решения вида (8) определены на всем бесконечном интервале  .
.
Вопрос о том, как отыскать все решения уравнения (7), решается нижеследующей теоремой:
Теорема 7. Допустим, что детерминант D(p) системы (6) не обращается тождественно в нуль, и пусть 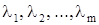 - совокупность всех различных корней многочлена D(p). Тогда произвольное решение х уравнения (7), может быть записано в виде:
- совокупность всех различных корней многочлена D(p). Тогда произвольное решение х уравнения (7), может быть записано в виде:
 (12)
(12)
где  — некоторое решение уравнения (7), соответствующее корню
— некоторое решение уравнения (7), соответствующее корню  (см. В)). Отсюда, в частности, следует, что каждое решение уравнения (7), определено для всех значений t.
(см. В)). Отсюда, в частности, следует, что каждое решение уравнения (7), определено для всех значений t.
Доказательство. Допустим, что  - некоторое решение уравнения (7) определенное на интервале
- некоторое решение уравнения (7) определенное на интервале  ; покажем, что на этом интервале оно может быть записано в виде (12). В силу предложения Б), каждая функция
; покажем, что на этом интервале оно может быть записано в виде (12). В силу предложения Б), каждая функция  , на интервале
, на интервале 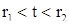 удовлетворяет уравнению
удовлетворяет уравнению

и потом в силу предложения А) § 6 может быть записана на этом интервале в виде:
 (13)
(13)
Здесь  есть многочлен степени
есть многочлен степени  , где
, где  — кратность корня
— кратность корня  .
.
Таким образом, каждое решение х уравнения (7) на интервале своего определения  записывается в виде:
записывается в виде:
 (14)
(14)
где  — вектор, компоненты которого являются многочленами степени
— вектор, компоненты которого являются многочленами степени  . Для доказательства теоремы 7 нам достаточно показать теперь, что каждое слагаемое
. Для доказательства теоремы 7 нам достаточно показать теперь, что каждое слагаемое  в правой части равенства (14) есть решение уравнения (7). Для доказательства этого подставим решение (14) в уравнение (7). Мы получим:
в правой части равенства (14) есть решение уравнения (7). Для доказательства этого подставим решение (14) в уравнение (7). Мы получим:
 (15)
(15)
Так как числа 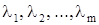 попарно различны, то из равенства (15) следует:
попарно различны, то из равенства (15) следует:
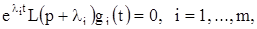
или, иначе,

Но это и значит, что 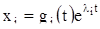 есть решение уравнения (7).
есть решение уравнения (7).
Итак, теорема 7 доказана.
Пример
Решим методом исключения систему уравнений

Перепишем ее в символической форме:

Детерминант системы, как легко видеть, равен  ; он имеет двукратный корень
; он имеет двукратный корень  . Согласно теореме 7 решение системы следует искать в виде:
. Согласно теореме 7 решение системы следует искать в виде:

Подстановка этих функций в первое уравнение дает (после сокращения на  ):
):
a + c – ct – d = 0,
откуда

Те же соотношения для коэффициентов получаются и при подстановке во второе уравнение системы. Таким образом, общее решение рассматриваемой системы записывается в виде:

где a и b - произвольные постоянные.
|
из
5.00
|
Обсуждение в статье: Линейное неоднородное уравнение с постоянными коэффициентами |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

