 |
Главная |
Автономные системы дифференциальных уравнений и их фазовые пространства
|
из
5.00
|
Здесь будет дана геометрическая интерпретация автономной системы уравнений в виде фазового пространства этой системы. Эта интерпретация существенно отличается от геометрической интерпретации системы уравнений, указанной в §§ 1, 2 и правильнее должна называться не геометрической, а кинематической, так как в этой интерпретации каждому решению системы уравнений ставится в соответствие не кривая в пространстве, а движение точки по кривой. Кинематическая интерпретация (фазовое пространство) в некоторых отношениях более выразительна, чем геометрическая (система интегральных кривых).
Автономные системы
Система обыкновенных дифференциальных уравнений называется автономной, если в нее явно не входит независимое переменное (или, как мы будем говорить, время) t. Это значит, что закон изменения неизвестных функций, описываемый системой уравнений не меняется с течением времени, как это обычно и бывает с физическими законами. Очень легко доказывается, что если
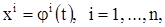
есть решение некоторой автономной системы уравнений, то
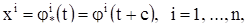
где с — константа, также есть решение той же автономной системы уравнений. Проведем доказательство этого факта на примере нормальной автономной системы уравнений,
А) Пусть
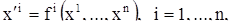 (1)
(1)
- автономная нормальная система уравнений порядка n и
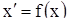
- векторная ее запись. Автономность системы (1) заключается в том, что функции 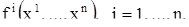 являются функциями переменных
являются функциями переменных 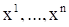 и не зависят от времени t. Относительно функций
и не зависят от времени t. Относительно функций 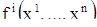 мы будем предполагать, что они определены на некотором открытом множестве
мы будем предполагать, что они определены на некотором открытом множестве  пространства размерности n, где координатами точки являются переменные
пространства размерности n, где координатами точки являются переменные 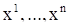 . Мы будем предполагать, что функции
. Мы будем предполагать, что функции 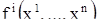 и их частные производные первого порядка непрерывны на множестве
и их частные производные первого порядка непрерывны на множестве 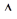 . Оказывается, что если
. Оказывается, что если
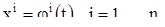 (2)
(2)
решение уравнения (1), то
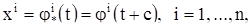 (3)
(3)
также есть решение системы (1).
Из правила дифференцирования сложной функции вытекает соотношение
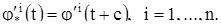 (4)
(4)
Действительно,
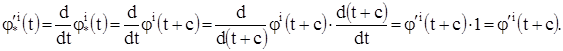
Докажем теперь, что (3) есть решение системы (1). Так как (2) есть решение, то мы имеем тождества
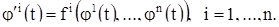
Заменяя в этих тождества t через t + c, мы получаем:
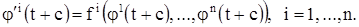
Из этого в силу (4) и (3) вытекает
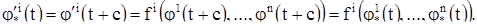
Перейдем теперь к кинематической интерпретации решений системы (1). Формально речь будет идти об интерпретации в n – мерном пространстве, но для наглядности разумно представлять себе случай плоскости (n = 2).
Б) Каждому решению
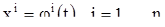 (5)
(5)
автономной системы (1) поставим в соответствие движение точки в n-мерном пространстве, задаваемое уравнениями (5), где 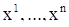 — координаты точки в пространстве, а t — время. В процессе своего движения точка описывает некоторую кривую — траекторию движения. Если сопоставить решению (5) не процесс движения, а траекторию движения точки, то мы получим менее полное представление о решении, поэтому желательно на траектории указать хотя бы направление движения. Оказывается, что если наряду с решением (5) имеется другое решение
— координаты точки в пространстве, а t — время. В процессе своего движения точка описывает некоторую кривую — траекторию движения. Если сопоставить решению (5) не процесс движения, а траекторию движения точки, то мы получим менее полное представление о решении, поэтому желательно на траектории указать хотя бы направление движения. Оказывается, что если наряду с решением (5) имеется другое решение
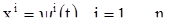 (6)
(6)
то траектории, соответствующие этим решениям, либо не пересекаются в пространстве, либо совпадают. Именно, если траектории имеют хотя бы одну общую точку, т. е.
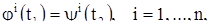 (7)
(7)
то
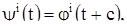 где
где 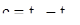 (8)
(8)
Последние равенства показывают, что траектории, описываемые первым и вторым решениями, совпадают между собой, но первое решение описывает ту же самую траекторию, что и второе, с «запозданием» на время с. Если точка, соответствующая первому решению, достигла некоторого положения на траектории в момент времени t + c, то точка, соответствующая второму решению, уже побывала в том положении в момент времени t.
Для того чтобы вывести из равенства (7) тождество (8), рассмотрим наряду с решением (5) решение
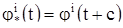 (9)
(9)
(см. А)). Из равенства (7) при 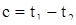 следует равенство
следует равенство
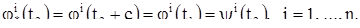
Таким образом, решения (6) и (9) системы (1) имеют общие начальные условия (а именно, значения в момент времени 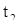 ) и потому в силу теоремы единственности совпадают, так что мы имеем:
) и потому в силу теоремы единственности совпадают, так что мы имеем:
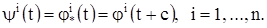
Положения равновесия и замкнутые траектории
Поставим вопрос о том, может ли траектория, изображающая решение системы, пересекать себя.
В) Пусть
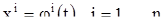 (10)
(10)
некоторое решение системы (1). Допустим, что имеет место равенство
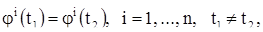 (11)
(11)
где числа 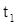 и
и 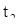 , конечно, принадлежат интервалу
, конечно, принадлежат интервалу 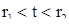 определения решения (10). Оказывается, что при этом условии решение (10) может быть продолжено на весь бесконечный интервал
определения решения (10). Оказывается, что при этом условии решение (10) может быть продолжено на весь бесконечный интервал 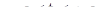 . Поэтому мы сразу будем считать, что само решение (10) определено на этом интервале
. Поэтому мы сразу будем считать, что само решение (10) определено на этом интервале 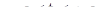 . Оказывается далее, что возможны два следующих взаимно исключающих случая.
. Оказывается далее, что возможны два следующих взаимно исключающих случая.
1) Для всех значений t имеет место равенство
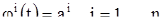
где 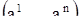 есть точка множества
есть точка множества 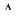 , не зависящая от t. Таким образом, в этом случае точка
, не зависящая от t. Таким образом, в этом случае точка 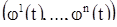 в действительности не движется при изменении t, а стоит на месте. Само решение (10) и точка
в действительности не движется при изменении t, а стоит на месте. Само решение (10) и точка 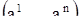 в этом случае называются положением равновесия системы (1).
в этом случае называются положением равновесия системы (1).
2) Существует такое положительное число Т, что при произвольном t имеют место равенства
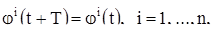
но при 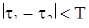 хотя бы для одного
хотя бы для одного 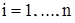 имеет место неравенство
имеет место неравенство
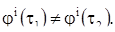
В этом случае решение (10) называется периодическим с периодом Т, а траектория, описываемая решением (10), называется замкнутой траекторией, или циклом.
Докажем предложение В). Как было отмечено в предложении Б) из равенств (11) следуют тождества
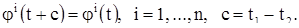 (12)
(12)
При этом функции 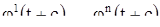 также представляют решение системы (1) (см. А)). Это решение и первоначальное решение (10) совпадают там, где они оба определены (теорема 2). Если объединить эти два решения, мы получим новое решение с большим интервалом существования, чем исходное, а именно, с интервалом
также представляют решение системы (1) (см. А)). Это решение и первоначальное решение (10) совпадают там, где они оба определены (теорема 2). Если объединить эти два решения, мы получим новое решение с большим интервалом существования, чем исходное, а именно, с интервалом 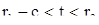 при с>0 и
при с>0 и 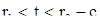 при с<0. Так как
при с<0. Так как 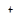 и
и 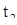 равноправны, то знак величины с можно изменить, так что решение можно продолжить, на интервал
равноправны, то знак величины с можно изменить, так что решение можно продолжить, на интервал 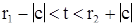 . Так как, кроме того, для продолженного решения равенство (11) по-прежнему выполнено, то к нему опять можно применить указанный способ расширения интервала существования, и потому мы можем продолжить решение (10) на всю бесконечную прямую с сохранением для него тождества (12).
. Так как, кроме того, для продолженного решения равенство (11) по-прежнему выполнено, то к нему опять можно применить указанный способ расширения интервала существования, и потому мы можем продолжить решение (10) на всю бесконечную прямую с сохранением для него тождества (12).
Каждое число с, для которого выполнено тождество (12), будем называть периодом решения (10); множество всех периодов решения (10) обозначим через F. Множество F есть некоторое множество чисел. Установим некоторые его свойства. Заменяя в соотношении (12) t через t - с, получаем 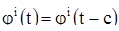 . Таким образом, если с есть период, то — с также есть период. Допустим, что
. Таким образом, если с есть период, то — с также есть период. Допустим, что 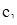 и
и 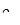 — периоды, т. е.
— периоды, т. е.
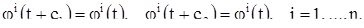
Тогда
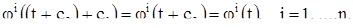
Таким образом, если 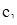 и
и 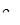 суть периоды, то
суть периоды, то 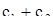 также есть период. Допустим, что
также есть период. Допустим, что 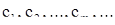 есть последовательность периодов, сходящаяся к некоторому числу
есть последовательность периодов, сходящаяся к некоторому числу 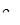 ; тогда мы имеем
; тогда мы имеем
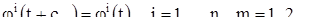
Так как функции 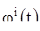 непрерывны, то при
непрерывны, то при  мы получаем:
мы получаем:
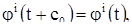
т.е. мы видим, что 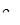 также есть период, так что множество F замкнуто.
также есть период, так что множество F замкнуто.
Так как число с в равенстве (12) отлично от нуля 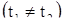 , то множество F содержит числа, отличные от нуля. Из установленных свойств множества F легко выводится, что для него есть только две возможности: 1) множество F совпадает с множеством всех действительных чисел; 2) в множестве F имеется минимальное положительное число Т, и тогда F состоит из всех целочисленных кратных числа Т. Докажем, что действительно имеются только эти две возможности. Так как множество F вместе с каждым числом с содержит число – с и так как в F имеются числа, отличные от нуля, то в F имеются положительные числа.
, то множество F содержит числа, отличные от нуля. Из установленных свойств множества F легко выводится, что для него есть только две возможности: 1) множество F совпадает с множеством всех действительных чисел; 2) в множестве F имеется минимальное положительное число Т, и тогда F состоит из всех целочисленных кратных числа Т. Докажем, что действительно имеются только эти две возможности. Так как множество F вместе с каждым числом с содержит число – с и так как в F имеются числа, отличные от нуля, то в F имеются положительные числа.
Допустим, что в множестве F нет наименьшего положительного числа, т. е. что для произвольного положительного числа 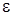 имеется положительный период с<
имеется положительный период с< 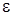 . Из доказанных свойств множества F следует (так как с есть период), что все числа mc, где m — целое, также являются периодами. Так как с<
. Из доказанных свойств множества F следует (так как с есть период), что все числа mc, где m — целое, также являются периодами. Так как с< 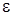 , то для произвольного действительного числа
, то для произвольного действительного числа 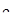 можно подобрать такое целое m, что
можно подобрать такое целое m, что 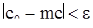 . Таким образом, произвольное число
. Таким образом, произвольное число 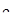 является предельным для множества F, и потому, ввиду замкнутости множества F, это множество совпадает с множеством всех действительных чисел.
является предельным для множества F, и потому, ввиду замкнутости множества F, это множество совпадает с множеством всех действительных чисел.
Допустим теперь, что F не есть множество всех действительных чисел. В силу доказанного, в F имеется тогда наименьшее положительное число Т. Пусть с — произвольный период. Можно тогда выбрать такое целое число m, что 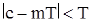 . Допустим, что
. Допустим, что 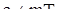 ; тогда
; тогда 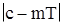 есть отличный от нуля период, а это невозможно, так как
есть отличный от нуля период, а это невозможно, так как 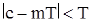 , что противоречит минимальности числа Т. Итак, доказано, что каждое число с из F может быть записано в виде c = mТ, где m — целое число.
, что противоречит минимальности числа Т. Итак, доказано, что каждое число с из F может быть записано в виде c = mТ, где m — целое число.
Теперь уже легко проверить, что если F есть множество всех действительных чисел, то имеет место случай 1), а если F не есть множество действительных чисел, то имеет место случай 2). Таким образом, предложение В) доказано.
Кратко предложение В) можно сформулировать, сказав, что имеется три сорта траекторий: 1) положение равновесия; 2) периодические траектории (циклы); 3) траектории без самопересечений. Естественно считать, что последний случай является «наиболее общим».
Из теоремы 2 следует, что через каждую точку области 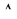 задания системы (1) проходит траектория, изображающая решение системы.
задания системы (1) проходит траектория, изображающая решение системы.
Таким образом, вся область 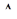 заполнена траекториями, причем, согласно Б), траектории эти попарно не пересекаются. Среди всех траекторий особо выделяются самопересекающиеся, которые являются либо положениями равновесия, либо циклами. Эти два сорта траекторий имеют весьма важное значение.
заполнена траекториями, причем, согласно Б), траектории эти попарно не пересекаются. Среди всех траекторий особо выделяются самопересекающиеся, которые являются либо положениями равновесия, либо циклами. Эти два сорта траекторий имеют весьма важное значение.
Такова кинематическая интерпретация решений автономной системы уравнений. Сама система уравнений также допускает геометрическую интерпретацию.
Фазовые пространства
Г) Поскольку автономная система уравнений (1) определена на открытом множестве 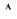 , каждой точке
, каждой точке 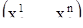 множества
множества 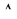 поставлена в соответствие последовательность из n чисел, именно последовательность:
поставлена в соответствие последовательность из n чисел, именно последовательность:
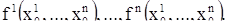
Эти числа можно рассматривать как компоненты вектора 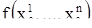 , проведенного в n-мерном пространстве и выходящего из точки
, проведенного в n-мерном пространстве и выходящего из точки 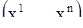 . Таким образом, автономной системе ставится в соответствие геометрический образ — векторное поле, заданное на открытом множестве
. Таким образом, автономной системе ставится в соответствие геометрический образ — векторное поле, заданное на открытом множестве 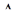 . В каждой точке
. В каждой точке 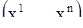 множества
множества 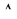 определен вектор
определен вектор 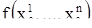 , выходящий из этой точки. Связь между геометрической интерпретацией решений и геометрической интерпретацией самой системы уравнений заключается в следующем. Пусть
, выходящий из этой точки. Связь между геометрической интерпретацией решений и геометрической интерпретацией самой системы уравнений заключается в следующем. Пусть 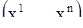 - произвольная точка множества
- произвольная точка множества 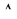 . В силу геометрической интерпретации системы уравнений этой точке поставлен в соответствие выходящий из нее вектор
. В силу геометрической интерпретации системы уравнений этой точке поставлен в соответствие выходящий из нее вектор 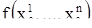 . Далее, в силу теоремы 2 существует решение
. Далее, в силу теоремы 2 существует решение 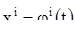 системы (1), удовлетворяющее начальным условиям
системы (1), удовлетворяющее начальным условиям
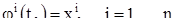
В силу кинематической интерпретации решению 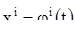 соответствует в пространстве движение точки, описывающее траекторию, причем в момент времени
соответствует в пространстве движение точки, описывающее траекторию, причем в момент времени 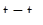 движущая точка проходит через положение
движущая точка проходит через положение 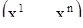 в пространстве. Оказывается, что векторная скорость точки, описывающей решение
в пространстве. Оказывается, что векторная скорость точки, описывающей решение 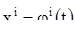 , в момент ее прохождения через положение
, в момент ее прохождения через положение 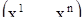 совпадает с вектором
совпадает с вектором 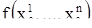 . Именно это совпадение и выражается системой уравнений (1) при
. Именно это совпадение и выражается системой уравнений (1) при
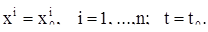
Пространство размерности n, в котором интерпретируются решения автономной системы (1) в виде траекторий и сама автономная система (1) в виде векторного поля, называется фазовым пространством системы (1). Траектории называются фазовыми траекториями, векторы 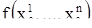 называются фазовыми скоростями. Связь между обеими интерпретациями заключается в том, что скорость движения точки по траектории в каждый момент времени совпадает с фазовой скоростью, заданной в том месте пространства, где в этот момент находится движущаяся точка.
называются фазовыми скоростями. Связь между обеими интерпретациями заключается в том, что скорость движения точки по траектории в каждый момент времени совпадает с фазовой скоростью, заданной в том месте пространства, где в этот момент находится движущаяся точка.
Рассмотрим теперь положения равновесия с точки зрения фазовых скоростей.
Д) Для того чтобы точка 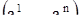 множества
множества  была положением равновесия системы (1), т. е. чтобы имелось решение
была положением равновесия системы (1), т. е. чтобы имелось решение 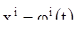 системы, для которого
системы, для которого
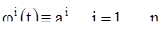 (13)
(13)
необходимо и достаточно, чтобы фазовая скорость 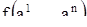 в точке
в точке 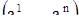 была равна нулю. Таким образом, для отыскания всех положений равновесия системы (1) нужно решить систему уравнений
была равна нулю. Таким образом, для отыскания всех положений равновесия системы (1) нужно решить систему уравнений
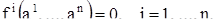
Эта система представляет собой не систему дифференциальных уравнений, а, как говорят, систему конечных уравнений (производные в нее не входят).
Для доказательства утверждения Д) допустим, что 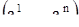 есть положение равновесия, т. е. что имеется решение
есть положение равновесия, т. е. что имеется решение 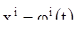 , для которого выполнены соотношения (13), и подставим в систему (1) это решение. Так как производная постоянной равна нулю, то подстановка дает
, для которого выполнены соотношения (13), и подставим в систему (1) это решение. Так как производная постоянной равна нулю, то подстановка дает
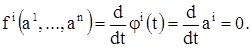
Таким образом, вектор 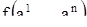 фазовой скорости действительно обращается в нуль, в точке
фазовой скорости действительно обращается в нуль, в точке 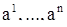 . Допустим, что, обратно, вектор
. Допустим, что, обратно, вектор 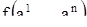 фазовой скорости обращается в нуль в точке
фазовой скорости обращается в нуль в точке 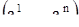 , т. е. что
, т. е. что 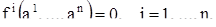 и покажем, что в этом случае равенства (13) определяют решение системы (1). Подстановка дает
и покажем, что в этом случае равенства (13) определяют решение системы (1). Подстановка дает
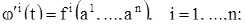
равенства эти выполнены, так как слева стоит производная константы, а справа — нуль.
Е) Геометрическая интерпретация решения (2) системы уравнений (1), указанная в §2, ставит в соответствие этому решению кривую К в (n + 1)-мерном пространстве переменных 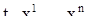 , определяемую системой уравнений (2). Здесь t является одной из координат в пространстве R. Переход к интерпретации в n-мерном фазовом пространстве S переменных
, определяемую системой уравнений (2). Здесь t является одной из координат в пространстве R. Переход к интерпретации в n-мерном фазовом пространстве S переменных 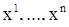 заключается в том, что мы перестаем считать величину t координатой точки, а считаем ее параметром. Таким образом, фазовая траектория L получается из кривой К в результате проектирования пространства R на пространство S в направлении оси t.
заключается в том, что мы перестаем считать величину t координатой точки, а считаем ее параметром. Таким образом, фазовая траектория L получается из кривой К в результате проектирования пространства R на пространство S в направлении оси t.
Геометрическую наглядность это проектирование приобретает при n = 2. В этом случае пространство R трехмерно, а пространство S представляет собой плоскость (см. пример 4).
Примеры
1. Рассмотрим автономное дифференциальное уравнение
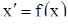 (14)
(14)
первого порядка, правая часть которого непрерывна и имеет непрерывную производную на всей прямой Р изменения переменного х. Предположим дополнительно, что нули функции f(x) или, что то же самое, положения равновесия уравнения (14), не имеют предельных точек. В этом предположении положения равновесия разбивают прямую Р на систему 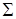 интервалов. Каждый интервал (a, b) системы
интервалов. Каждый интервал (a, b) системы 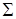 обладает тем свойством, что на нем функция f (x) не обращается в нуль, а каждый конец a или b его является либо нулем функции f (x), либо равен
обладает тем свойством, что на нем функция f (x) не обращается в нуль, а каждый конец a или b его является либо нулем функции f (x), либо равен  . Таким образом, система
. Таким образом, система 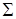 состоит из конечного или счетного числа конечных интервалов и не более чем двух полубесконечных интервалов или же содержит только один бесконечный в обе стороны интервал
состоит из конечного или счетного числа конечных интервалов и не более чем двух полубесконечных интервалов или же содержит только один бесконечный в обе стороны интервал  . Пусть (a, b) - некоторый интервал системы
. Пусть (a, b) - некоторый интервал системы 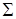 ,
, 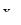 - точка этого интервала и
- точка этого интервала и 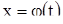 ,
, 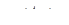 , - непродолжаемое решение уравнения (14) с начальными значениями 0,
, - непродолжаемое решение уравнения (14) с начальными значениями 0, 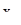 . Допустим для определенности, что
. Допустим для определенности, что 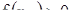 ; тогда оказывается, что
; тогда оказывается, что
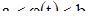 при
при 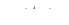 , (15)
, (15)
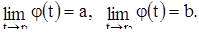 (16)
(16)
Далее, если число а, или соответственно b, конечно, то число 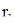 или соответственно
или соответственно 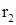 , бесконечно. Таким образом (рис. 3), каждый интервал (a, b) представляет собой одну-единственную фазовую траекторию уравнения (14).
, бесконечно. Таким образом (рис. 3), каждый интервал (a, b) представляет собой одну-единственную фазовую траекторию уравнения (14).
Докажем соотношения (15), (16). Из предположения 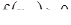 следует, что на интервале (a, b) функция f (x) положительна и потому каждая точка этого интервала, описывая фазовую траекторию, движется слева направо. Таким образом, при возрастающем t точка
следует, что на интервале (a, b) функция f (x) положительна и потому каждая точка этого интервала, описывая фазовую траекторию, движется слева направо. Таким образом, при возрастающем t точка 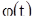 может покинуть интервал (a, b), лишь перейдя его правый конец b. Допустим, что это происходит при некотором
может покинуть интервал (a, b), лишь перейдя его правый конец b. Допустим, что это происходит при некотором 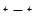 ; тогда при
; тогда при 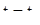 имеем
имеем 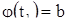 , а это значит, что две различные траектории
, а это значит, что две различные траектории 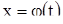 и x = b пересекаются, что невозможно. Точно так же доказывается, что точка
и x = b пересекаются, что невозможно. Точно так же доказывается, что точка 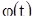 не может покинуть интервал (a,b) при убывающем t. Таким образом, соотношение (15) доказано.
не может покинуть интервал (a,b) при убывающем t. Таким образом, соотношение (15) доказано.
Допустим теперь, что 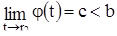 и пусть
и пусть 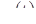 — решение уравнения (14) с начальными значениями 0, с. Так как f (с)> 0, то при некотором отрицательном значении
— решение уравнения (14) с начальными значениями 0, с. Так как f (с)> 0, то при некотором отрицательном значении 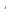 имеем
имеем 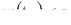 , а это значит, что две различные траектории
, а это значит, что две различные траектории 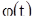 и
и 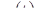 пересекаются, что невозможно. Таким образом, доказано, что
пересекаются, что невозможно. Таким образом, доказано, что 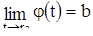 . Точно так же доказывается и соотношение
. Точно так же доказывается и соотношение 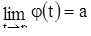 .
.
Допустим, наконец, что  , и покажем, что тогда
, и покажем, что тогда 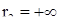 . Допустим противоположное, именно, что
. Допустим противоположное, именно, что 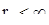 . Определим тогда функцию
. Определим тогда функцию 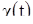 , положив
, положив 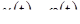 при
при 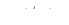 и
и 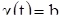 при
при 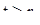 . Очевидно, что функция
. Очевидно, что функция 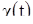 непрерывна и удовлетворяет уравнению (14), а это невозможно, так как тогда пересекаются две различные траектории
непрерывна и удовлетворяет уравнению (14), а это невозможно, так как тогда пересекаются две различные траектории 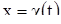 и
и  . Полученное противоречие показывает, что
. Полученное противоречие показывает, что 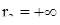 . Точно так же доказывается, что при
. Точно так же доказывается, что при 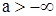 имеем
имеем 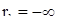 .
.
Пусть b — произвольное положение равновесия уравнения (14), а (a, b) и (b, c) — два интервала системы 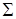 , примыкающие к нему (соответственно слева и справа). Каждый из интервалов (a, b), (b, c) представляет собой одну траекторию. Если обе точки, описывающие траектории (a, b) и (b, c), приближаются (при возрастании t) к положению равновесия b, то положение равновесия b называется устойчивым (рис. 4, а). Если обе точки, описывающие траектории (a, b) и (b, c), удаляются от точки b, то положение равновесия b называется неустойчивым (рис 4, б). Если по одной из траекторий точка приближается, а по другой удаляется, то положение равновесия b называется полуустойчивым (рис. 4, в). Для того чтобы положение равновесия b было устойчивым, необходимо и достаточно, чтобы функция f (x) была положительна на интервале (a, b) и отрицательна на интервале (b, c). Для того чтобы положение равновесия b было неустойчивым, необходимо и достаточно, чтобы функция f (х) была отрицательна на интервале (a, b) и положительна на интервале (b, c). Для того чтобы положение равновесия b было полуустойчиво, необходимо и достаточно, чтобы функция f (х) имела один и тот же знак на обоих интервалах (a, b) и (b,c).
, примыкающие к нему (соответственно слева и справа). Каждый из интервалов (a, b), (b, c) представляет собой одну траекторию. Если обе точки, описывающие траектории (a, b) и (b, c), приближаются (при возрастании t) к положению равновесия b, то положение равновесия b называется устойчивым (рис. 4, а). Если обе точки, описывающие траектории (a, b) и (b, c), удаляются от точки b, то положение равновесия b называется неустойчивым (рис 4, б). Если по одной из траекторий точка приближается, а по другой удаляется, то положение равновесия b называется полуустойчивым (рис. 4, в). Для того чтобы положение равновесия b было устойчивым, необходимо и достаточно, чтобы функция f (x) была положительна на интервале (a, b) и отрицательна на интервале (b, c). Для того чтобы положение равновесия b было неустойчивым, необходимо и достаточно, чтобы функция f (х) была отрицательна на интервале (a, b) и положительна на интервале (b, c). Для того чтобы положение равновесия b было полуустойчиво, необходимо и достаточно, чтобы функция f (х) имела один и тот же знак на обоих интервалах (a, b) и (b,c).
Допустим, что 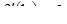 ; тогда знак функции f (х) вблизи точки b совпадает со знаком величины
; тогда знак функции f (х) вблизи точки b совпадает со знаком величины 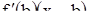 . Отсюда следует, что при
. Отсюда следует, что при 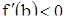 положение равновесия b уравнения (14) устойчиво, а при
положение равновесия b уравнения (14) устойчиво, а при 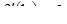 оно неустойчиво.
оно неустойчиво.
2. Рассмотрим уравнение
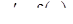 (17)
(17)
где f (x) есть периодическая функция с непрерывной первой производной. Для определенности будем считать, что период ее равен 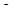 . Все сказанное в примере 1 относительно уравнения (14) остается правильным и для уравнения (17), так как уравнение (17) является частным случаем уравнения (14). Однако, для того чтобы учесть специфику уравнения (17) (периодичность функций f (x)) разумно считать, что фазовым пространством уравнения (17) является не прямая, а окружность К радиуса единица, на которой выбрано некоторое начало отсчета 0 и направление обхода (например, против часовой стрелки). Каждому числу х поставим в соответствие точку
. Все сказанное в примере 1 относительно уравнения (14) остается правильным и для уравнения (17), так как уравнение (17) является частным случаем уравнения (14). Однако, для того чтобы учесть специфику уравнения (17) (периодичность функций f (x)) разумно считать, что фазовым пространством уравнения (17) является не прямая, а окружность К радиуса единица, на которой выбрано некоторое начало отсчета 0 и направление обхода (например, против часовой стрелки). Каждому числу х поставим в соответствие точку 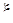 окружности К, отложив от начала отсчета против часовой стрелки дугу длины х (рис. 5). При этом всем числам
окружности К, отложив от начала отсчета против часовой стрелки дугу длины х (рис. 5). При этом всем числам 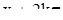 (k – целое число) будет соответствовать на окружности одна и та же точка
(k – целое число) будет соответствовать на окружности одна и та же точка 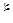 . Так как f(
. Так как f( 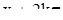 ) = f(x), то можно положить f(
) = f(x), то можно положить f( 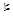 ) = f(x), и функция f оказывается заданной на окружности К.
) = f(x), и функция f оказывается заданной на окружности К.
Уравнение (17) задает теперь движение точки 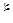 по окружности К. Если x(t) есть некоторое решение уравнения (17), то соответствующая числу x(t) точка
по окружности К. Если x(t) есть некоторое решение уравнения (17), то соответствующая числу x(t) точка 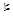 (t) движется по окружности К. Если
(t) движется по окружности К. Если 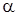 — такая точка на окружности К, что f (
— такая точка на окружности К, что f ( 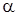 ) = 0, то существует такое решение x(t) уравнения (17), что
) = 0, то существует такое решение x(t) уравнения (17), что 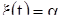 , и
, и 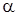 есть положение равновесия уравнения (17). Допустим для простоты, что положения равновесия уравнения (17) на окружности К не имеют предельных точек: тогда их имеется лишь конечное число или нет вовсе (рис. 6). Положения равновесия разбивают окружность на конечную систему
есть положение равновесия уравнения (17). Допустим для простоты, что положения равновесия уравнения (17) на окружности К не имеют предельных точек: тогда их имеется лишь конечное число или нет вовсе (рис. 6). Положения равновесия разбивают окружность на конечную систему 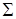 интервалов. Если положений равновесия вовсе нет, то система
интервалов. Если положений равновесия вовсе нет, то система 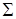 содержит лишь один «интервал» (окружность). Если имеется лишь одно положение равновесия
содержит лишь один «интервал» (окружность). Если имеется лишь одно положение равновесия 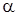 , то система
, то система 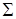 также содержит лишь один интервал, состоящий из всех точек окружности К за исключением точки
также содержит лишь один интервал, состоящий из всех точек окружности К за исключением точки 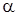 . В первом случае интервал вовсе не имеет концов, во втором оба его конца совпадают. Пусть I — некоторый интервал системы
. В первом случае интервал вовсе не имеет концов, во втором оба его конца совпадают. Пусть I — некоторый интервал системы 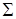 и x(t) — некоторое решение уравнения (17) с начальными значениями 0,
и x(t) — некоторое решение уравнения (17) с начальными значениями 0, 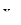 , где
, где 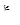 есть точка, интервала I. Решение x(t) всегда определено для всех значении t, и точка
есть точка, интервала I. Решение x(t) всегда определено для всех значении t, и точка 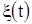 принадлежит интервалу I. Если интервал I имеет концы (один или два), то точка пробегает интервал I и определенном направлении, причем каждая точка интервала I проходится решением
принадлежит интервалу I. Если интервал I имеет концы (один или два), то точка пробегает интервал I и определенном направлении, причем каждая точка интервала I проходится решением 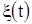 один раз. Если интервал I совпадает со всей окружностью, то, отправившись из положения
один раз. Если интервал I совпадает со всей окружностью, то, отправившись из положения 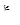 , точка через некоторое время Т вернется в нее, так что
, точка через некоторое время Т вернется в нее, так что 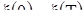 . В этом случае
. В этом случае 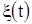 периодически зависит от числа t с периодом Т. Соответствующее движению
периодически зависит от числа t с периодом Т. Соответствующее движению 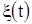 числовое решение x(t) уравнения (17) удовлетворяет условию
числовое решение x(t) уравнения (17) удовлетворяет условию

Из этого примера видно, что фазовым пространством системы уравнений не всегда целесообразно считать эвклидово координатное пространство, а иногда приходится считать более сложное геометрическое образование. Ниже, в примере 3, мы столкнемся с этим обстоятельством в более сложной обстановке, чем в этом примере.
3. Рассмотрим систему уравнений
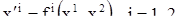 (18)
(18)
где функции 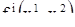 являются периодическими относительно обоих аргументов с периодами
являются периодическими относительно обоих аргументов с периодами 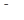 :
:
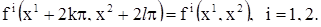
Как всегда, будем предполагать, что функции 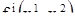 непрерывны и имеют непрерывные частные производные первого порядка. Ввиду периодичности функций
непрерывны и имеют непрерывные частные производные первого порядка. Ввиду периодичности функций 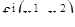 разумно считать, что фазовым пространством системы (18) является не плоскость, а более сложное геометрическое образование, именно, поверхность тора или, как говорят, тор (рис. 7). Опишем эту поверхность.
разумно считать, что фазовым пространством системы (18) является не плоскость, а более сложное геометрическое образование, именно, поверхность тора или, как говорят, тор (рис. 7). Опишем эту поверхность.
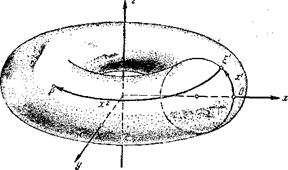
Рис. 7.
В трехмерном эвклидовом пространстве с декартовыми координатами х, у, z выберем в плоскости х, z окружность K радиуса единица с центром в точке (2, 0, 0). Примем на этой окружности за начало отсчета точку с координатами (3, 0, 0). Тогда каждому числу х будет поставлена в соответствие точка 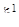 окружности К (см. пример 2). Будем теперь вращать плоскость (х, z) в пространстве (х, у, z) вокруг оси z. Описываемая при этом вращении окружностью К поверхность Р представляет собой тор. Пусть
окружности К (см. пример 2). Будем теперь вращать плоскость (х, z) в пространстве (х, у, z) вокруг оси z. Описываемая при этом вращении окружностью К поверхность Р представляет собой тор. Пусть 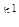 — некоторая точка окружности К. В результате поворота плоскости (х, z) на угол
— некоторая точка окружности К. В результате поворота плоскости (х, z) на угол 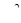 , исчисляемый в радианах, точка
, исчисляемый в радианах, точка 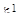 перейдет в некоторую точку р, тора Р (рис. 7). Если сделать поворот не на угол
перейдет в некоторую точку р, тора Р (рис. 7). Если сделать поворот не на угол 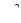 , а на угол
, а на угол  , то мы придем к той же точке р тора Р. Таким образом, точка р тора Р однозначно определяется двумя циклическими координатами
, то мы придем к той же точке р тора Р. Таким образом, точка р тора Р однозначно определяется двумя циклическими координатами 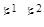 , и каждой паре циклических координат
, и каждой паре циклических координат 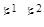 соответствует на торе одна вполне определенная точка. Мы видим, таким образом, что функции
соответствует на торе одна вполне определенная точка. Мы видим, таким образом, что функции 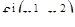 можно считать заданными не на плоскости, а на поверхности тора Р:
можно считать заданными не на плоскости, а на поверхности тора Р:
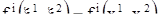
Пусть теперь 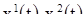 — некоторое решение системы (18). Ставя в соответствие каждому из чисел
— некоторое решение системы (18). Ставя в соответствие каждому из чисел 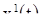 и
и 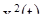 циклические координаты
циклические координаты 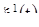 и
и 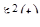 , мы получаем точку
, мы получаем точку 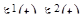 тора Р. Таким образом, каждое решении
тора Р. Таким образом, каждое решении 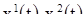 системы (18) может быть изображено движением точки по тору, причем закон движения в каждый момент времени определяется той точкой
системы (18) может быть изображено движением точки по тору, причем закон движения в каждый момент времени определяется той точкой 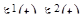 тора, через которую траектория в этот момент проходит. Это объясняется тем, что функции
тора, через которую траектория в этот момент проходит. Это объясняется тем, что функции 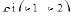 заданы на торе. Таким образом, весь тор Р оказывается покрытым траекториями, каждые две из которых либо не пересекаются либо совпадают. В частности, если траектория пересекает самое себя, то она либо замкнута, либо является положением равновесия.
заданы на торе. Таким образом, весь тор Р оказывается покрытым траекториями, каждые две из которых либо не пересекаются либо совпадают. В частности, если траектория пересекает самое себя, то она либо замкнута, либо является положением равновесия.
Изображение, фазовых траекторий системы (18) не на плоскости, а на поверхности тора отражает специфическое свойство системы (18) (периодичность функций  ) и удобно при ее изучении.
) и удобно при ее изучении.
4. Каждое решение автономной системы уравнений

записывается в виде:
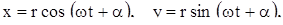 (19)
(19)
где r и 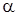 — константы. Система уравнений (19) определяет в трехмерном пространстве R переменных t, х, у винтовую спираль при
— константы. Система уравнений (19) определяет в трехмерном пространстве R переменных t, х, у винтовую спираль при 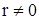 и прямую линию (именно, ось t) при r = 0.
и прямую линию (именно, ось t) при r = 0.
В фазовой плоскости S переменных х и у та же система уравнений (19) определяет окружность при 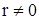 и точку (положение равновесия) при r = 0. Переход от кривых в пространстве R к кривым плоскости S осуществляется проектированием в направлении оси t на координатную плоскость ху.
и точку (положение равновесия) при r = 0. Переход от кривых в пространстве R к кривым плоскости S осуществляется проектированием в направлении оси t на координатную плоскость ху.
5. Каждое решение неавтономной системы уравнений


