Фазовая плоскость линейной однородной системы с постоянными коэффициентами

 

Здесь будут построены фазовые траектории на фазовой плоскости системы

 

 (1)

 

или в векторной форме

 

 (2)

 

с постоянными действительными коэффициентами . При этом нам придется разобрать, несколько различных случаев, так как фазовая картина траекторий системы существенно зависит от значении коэффициентов.

Следует заметить, что начало координат (точка (0, 0)) всегда является положением равновесия системы (1). Это положение равновесия тогда и только тогда является единственным, когда детерминант матрицы  отличен от нуля, или, что то же, оба собственных значения этой матрицы отличны от нуля.

Допустим, что собственные значения матрицы А действительны, различны и отличны от нуля. Тогда, как это следует из результатов § 9 (теорема 8) произвольное действительное решение уравнения (2) можно записать в виде:

 

 (3)

 

Здесь  и  — действительные линейно независимые собственные векторы матрицы А;  и  — его действительные собственные значения, а  и  — действительные константы. Решение (3) разложим по базису , положив

 

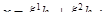 (4)

 

тогда мы будем иметь:

 

 (5)

 

Координаты  на фазовой плоскости Р системы (1) вообще говоря, не являются прямоугольными, поэтому отобразим аффинно фазовую плоскость Р на вспомогательную плоскость Р* таким образом чтобы при этом векторы ,  перешли во взаимно ортогональные единичные векторы плоскости Р*, направленные соответственно по оси абсцисс и оси ординат (рис. 8). Точка  плоскости Р перейдет при этом отображении в точку с декартовыми прямоугольными координатами  в плоскости Р*. Таким образом, траектория заданная, параметрическими уравнениями (5) а плоскости Р перейдет в траекторию (которую мы также назовем фазовой), заданную теми же уравнениями в прямоугольных координатах плоскости Р*. Мы начертим сперва траектории, заданные уравнениями (5) в плоскости Р*, и затем отобразим их обратно в плоскость Р.

 

 

Рис. 8.

 

Наряду с фазовой траекторией (5) в плоскости Р* имеется траек­тория, задаваемая уравнениями

 

 (6)

 

а также траектория, задаваемая уравнениями

 

 (7)

 

Траектория (6) получается из траектории (5) зеркальным отражением относительно оси абсцисс, а траектория (7) — относительно оси ординат. Таким образом, указанные два зеркальных отображения оставляют картину траекторий на плоскости Р* инвариантной. Из этого видно, что если вычертить траектории в первом квадранте, то уже легко представить себе всю фазовую картину в плоскости Р*.

Отметим что при  мы получаем движение точки, описывающее положение равновесия (0, 0). При  получаем движение, описывающее положительную полуось абсцисс, при  получаем движение, описывающее положительную полуось ординат. Если , то движение, описывающее положительную полуось абсцисс, протекает в направлении к началу координат, если же , то движение это имеет противоположное направление от начала координат. В первом случае точка движется, неограниченно приближаясь к началу координат, во второй — неограниченно удаляясь в бесконечность. То же справедливо и относительно движения, описывающего положительную полуось ординат. Если  и  положительны, то движение точки протекает в первой четверти, не выходя на ее границу.

Дальнейшее, более детальное описание фазовой плоскости проведем отдельно для нескольких случаев - в зависимости от знаков чисел .

А) Узел. Допустим, что оба числа  и отличны от нуля и имеют один знак, причем

 

 (8)

 

Разберем сперва случай, когда , .

При этих предположениях движение по положительной полуоси абсцисс направлено к началу координат, точно так же, как движе­ние по положительной полуоси ординат. Далее, движение по произ­вольной траектории внутри первого квадранта состоит в асимптотическом приближении точки к началу координат, причем траекто­рия при этом касается оси абсцисс в начале координат. При t, стремящемся к , точка движется так, что абсцисса и ордината ее бесконечно возрастают, но возрастание ординаты сильнее, чем воз­растание абсциссы, т. е. движение идет в направлении оси ординат. Эта фазовая картина называется устойчивом узлом (рис. 9, а). Если наряду с неравенством (8) выполнены неравенства

 

то траектории остаются прежними, но движение по ним направлено в противоположном направлении. Мы имеем неустойчивый узел (рис. 9, б).

 

 а) Рис. 9.                                 б)

 

 

Б) Седло. Допустим, что числа  и  имеют противоположные знаки. Для определенности предположим, что . В этом случае движение по положительной полуоси абсцисс идет к началу координат, а движение по положительной полуоси ординат — от начала координат. Траектории, лежащие внутри первого квадранта, напоминают по своему виду гиперболы, а движения по ним про­исходят в направлении к началу вдоль оси абсцисс, и в направлении от начала вдоль оси ординат. Эта фазовая картина называется седлом (рис. 10).

Рисунки 9, а, б и 10 дают картину траекторий на вспомогательной фазовой плоскости Р*. Расположение траекторий на фазовой плоскости Р получается из этого с помощью аффинного преобразования и зависят от положения собственных векторов (см., например, рис. 11 и 12).

Рассмотрим теперь случай, когда собственные значения матрицы А комплексны. В этом случае они комплексно сопряжены и могут быть обозначены через  и , причем . Собственные векторы матрицы А могут быть выбраны сопряженными, так что их можно обозначить через h и . Положим:

 

 

где  и  — действительные векторы. Векторы  и  линейно независимы, так как в случае линейной зависимости между ними мы имели бы линейную зависимость между h и . Итак, векторы  и  можно принять, за базис фазовой плоскости Р уравнения (2).

Произвольное действительное решение уравнения (2) можно записать в виде:

 

 (9)

 

где с — комплексная константа. Пусть

 

 

тогда мы имеем:

 

Отобразим аффинно фазовую плоскость Р на вспомогательную плоскость Р* комплексного переменного  так, чтобы вектор  перешел в единицу, а вектор  - в i; тогда вектору  будет соответствовать комплексное число . В силу этого отображения фазовая траектория (9) перейдет в фазовую траекторию на плоскости Р*, описываемую уравнением

 

 (10)

 

 Рис. 11. Рис. 12.

 

В) Фокус и центр. Перепишем уравнение (10) в полярных координатах, положив

 

 

Таким образом, получаем:

 

 

это есть уравнение движения точки в плоскости Р*. При  каждая траектория оказывается логарифмической спиралью. Соответствующая картина на плоскости Р называется фокусом. Если , то точка при возрастании t асимптотически приближается к началу координат, описывая логарифмическую спираль. Это – устойчивый фокус (рис. 13, а). Если , то точка уходит от начала координат в бесконечность, и мы имеем неустойчивый фокус (рис. 13, б). Если число  равно нулю, то каждая фазовая траектория, кроме положения равновесия (0,0), замкнута, и мы имеем так называемый центр (рис. 14).

 

    а)                    Рис. 13           б)

 

Рисунки 13 и 14 дают картину во вспомогательной фазовой плоскости; в плоскости Р картина аффинно искажается (см., например, рис. 15 и 16).

 

      

Рис. 14. Рис. 15.

 

Выше мы рассматривали так называемые невырожденные случаи: корни  и  различны и отличны от нуля. Малое изменение элементов матрицы  не меняет в этих предположениях общего характера поведения фазовых траекторий. Исключение составляет случай центра: при малом изменении элементов матрицы  равенство  может нарушиться, и центр перейдет в устойчивый или неустойчивый фокус.