Сведение обшей системы дифференциальных уравнений к нормальной

В предыдущем параграфе была сформулирована теорема существования и единственности для нормальной системы дифференциальных уравнений. Здесь будет показано, каким образом весьма общие системы дифференциальных уравнений сводятся к нормальным системам дифференциальных уравнений, и тем самым будет установлена теорема существования и единственности для этих общих систем уравнений.

Дадим сначала понятие о системе дифференциальных уравнений в общем виде.

В случае одной неизвестной функции х независимого переменного t обычно рассматривается одно уравнение, которое можно записать в виде:

 (1)

Здесь t — независимое переменное, х — его неизвестная функция, а F - заданная функция n+2 переменных. Функция F может быть задана не для всех значений ее аргументов, поэтому говорят об области В задания функции F. Здесь имеется в виду открытое множество В координатного пространства размерности n+2, в котором координатами точки являются переменные . Если максимальный порядок производной, входящей в дифференциальное уравнение, равен n, то говорят, что имеется уравнение n-го порядка. Решением уравнения (1) называется такая непрерывная функция  независимого переменного t, определенная на некотором интервале , что при подстановке ее вместо х в уравнение (1) мы получаем тождество по t на интервале . Очевидно, что подстановка  в соотношение (1) возможна лишь тогда, когда функция  на всем интервале своего существования  имеет производные до порядка n включительно. Для того чтобы подстановка  в соотношение (1) была возможна, необходимо также, чтобы точка, имеющая координаты , принадлежала множеству В определения функции F при произвольном t интервала .

Если имеются две неизвестные функции одного независимого переменного, то рассматриваются два дифференциальных уравнения, вместе образующих систему уравнений. Система эта может быть написаны в виде:

 (2)

Здесь t - независимое переменное, х и у — две его неизвестные функции, F и G - две функции, каждая от  переменных, заданные в некотором открытом множестве В. Если максимальный порядок производной функции х, входящей в систему (2), равен , м максимальный порядок производной функции у, входящей в систему (2), равен , то число  называется порядком системы (2) относительно х, число  — порядком системы (2) относительно у, а число  называется порядком системы (2). Решением си­стемы (2) называется пара непрерывных функций  и , заданных на некотором интервале  и обладающих тем свойством, что при подстановке их в соотношения (2) мы приходим к тождествам по t на всем интервале . Как и в случае одного уравнения, предполагаются выполненными условия, дающие возможность делать подстановку , , в систему (2).

Аналогично определяются системы дифференциальных уравнений с тремя и большим числом неизвестных функций от одного независимого переменного. Если неизвестными функциями системы дифференциальных уравнении являются функции 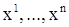, а наивысший порядок производной функции , входящей в систему, ра­вен 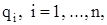 то число  называется порядком системы относительно , а число  называется поряд­ком системы. Таким образом, нормальная система (1) §2 имеет порядок n.

Если соотношение (1) может быть разрешено относительно , то уравнение (1) переписывается в виде:

 (3)

Точно так же, если система (2) может быть разрешена относительно величин  и , то эта система может быть переписана в виде:

 (4)

Уравнение (3) и система (4) называются разрешенными относительно высших производных. Аналогично определяются разрешенные относительно высших производных системы с произвольным числом неизвестных функций. В частности, нормальная система (1) § 2 является разрешенной относительно высших производных.

Покажем теперь, что всякая имеющая порядок n система дифференциальных уравнений, разрешенная относительно высших производных. сводится к нормальной системе порядка n. Для начала покажем, как одно уравнение порядка n сводится к нормальной системе по­рядка n.

А) Пусть

 (5)

- одно дифференциальное уравнение порядка n, разрешенное отно­сительно высшей производной. Здесь t — независимое переменное, у — неизвестная функция переменного t. Далее,  есть заданная функция n+1 переменных , определенная в некотором открытом множестве Г координатного пространства размерности n+1. Относительно функции  мы будем предполагать, что она непрерывна на множестве Г и что ее частные производные

(где предполагается, что ) также непрерывны на множестве Г. Для замены уравнения (5) нормальной системой уравнений вводятся новые неизвестные функции  независимого переменного t при помощи равенств

 (6)

Оказывается, что уравнение (5) эквивалентно системе

 (7)

Из этого в силу теоремы 2 следует, что для каждой точки  множества Г существует решение  уравнения (5), удовлетворяющее начальным условиям

или, как говорят, решение с начальными значениями

 (8)

Далее, любые два решения с начальными значениями (8) совпадают на общей части их интервалов определения. Если уравнение (5) линейно, т. е. функция f линейна относительно переменных , а коэффициенты ее определены и непрерывны на интервале , то для любых начальных значений , где  имеется решение , определенное на всем интервале .

Докажем, что уравнение (5) эквивалентно системе (7). Допустим, что функция у удовлетворяет уравнению (5), и докажем, что функции , определенные соотношениями (6), удовлетворяют системе (7). Дифференцируя соотношения (6), вводящие новые неизвестные функции 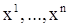, получаем:

 (9)

 (10)

Заменяя правые части соотношений (9) на основе соотношений (6), а правую часть соотношения (10) на основании уравнения (5), которому функция у удовлетворяет, мы получаем систему (7). Допустим, что, наоборот, функции  удовлетворяют системе (7); примем тогда  за у покажем, что функция у удовлетворяет уравнению (5). Полагая в первом из уравнении системы (7)  получаем 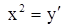. Заменяя во втором из уравнений (7)  через , получаем . Продолжая это построение дальше, мы приходим к соотношениям (6). Наконец, заменяя в последнем из уравнений системы (7) каждую функцию  в силу формул (6), получаем уравнение (5) для у.

Так как функция f определена на множестве Г, то правые части системы (7) также определены на множестве Г при условии замены координат по формулам (6). Для системы (7) выполнены условия теоремы 2 на множестве Г. Таким образом, можно произвольно выбрать начальные значения  в множестве Г. Эти начальные значения в силу замены (6) превращаются в начальные значения

для уравнения (5).

Если уравнение (5) линейно, то система (7) также линейна. Из этого в силу теоремы 3 вытекает заключительная часть предло­жения А). Таким образом, предложение А) доказано.

Прием, описанный в предложении А), дает возможность привести к нормальной системе произвольную систему дифференциальных уравнений, разрешенную относительно высших производных.