 |
Главная |
Линейное однородное уравнении с постоянными коэффициентами (случай простых корней)
|
из
5.00
|
В этом и следующем параграфах будет решено линейное однородное уравнение с постоянными коэффициентами порядка n, т. е. уравнение
 (1)
(1)
где z есть неизвестная функция независимого переменного t, а коэффициенты  суть постоянные числа (действительные или комплексные). Сначала будут найдены все комплексные решения этого уравнения, а затем (в случае, когда коэффициенты
суть постоянные числа (действительные или комплексные). Сначала будут найдены все комплексные решения этого уравнения, а затем (в случае, когда коэффициенты  действительны) из них будут выделены действительные решения. Уравнение (1) можно записать в виде:
действительны) из них будут выделены действительные решения. Уравнение (1) можно записать в виде:
 (2)
(2)
так что к нему применима теорема существования и единственности. В дальнейшем будет использована лишь единственность, так как решения уравнения (2) будут найдены явно и тем самым существование их будет установлено; единственность же будет использована для доказательства того, что найдены все решения.
В инженерных применениях обыкновенных дифференциальных уравнений с постоянными коэффициентами важную роль играет операционное исчисление. Мы используем здесь символические (или, иначе, операционные) обозначения, лежащие в основе операционного исчисления. Суть этих обозначений заключается в том, что производная по времени t, от произвольной функции  обозначается не через
обозначается не через  , а через
, а через  , так что буква р, стоящая слева от функции, является символом дифференцирования по t. Если позволить себе применить к символу дифференцирования р некоторые алгебраические действия, то мы приходим к обозначению
, так что буква р, стоящая слева от функции, является символом дифференцирования по t. Если позволить себе применить к символу дифференцирования р некоторые алгебраические действия, то мы приходим к обозначению

Пользуясь этим обозначением, мы можем написать

Если теперь в правой части последнего равенства позволить себе вынести за скобку функцию z, то мы получаем равенство

Таким образом, мы приходим к формальному определению.
А) Пусть

- произвольный многочлен относительно символа р с постоянными коэффициентами (действительными или комплексными) и z — некоторая действительная или комплексная функция действительного переменного t. Положим:
 (3)
(3)
Если  и
и  суть два произвольных многочлена относительно символа р (или, как говорят, оператора дифференцирования р), а
суть два произвольных многочлена относительно символа р (или, как говорят, оператора дифференцирования р), а  — функции переменного t, то, как легко видеть, мы имеем тождества
— функции переменного t, то, как легко видеть, мы имеем тождества
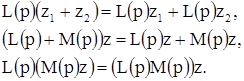
В силу введенных обозначений уравнение (1) может быть записано в виде:
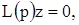 (4)
(4)
где

Б) Пусть  — произвольный многочлен относительно символа р. Тогда
— произвольный многочлен относительно символа р. Тогда
 (5)
(5)
Докажем формулу (5). Мы имеем

Из этого следует, что  . Отсюда формула (5) вытекает непосредственно (см. (3)).
. Отсюда формула (5) вытекает непосредственно (см. (3)).
Из формулы (5) следует, что функция  тогда и только тогда является решением уравнения (4), когда число
тогда и только тогда является решением уравнения (4), когда число  есть корень многочлена
есть корень многочлена  . Многочлен
. Многочлен  называется характеристическим многочленом уравнения (4). В том случае, когда он не имеет кратных корней, совокупность всех решений уравнения (4) описывается следующей теоремой.
называется характеристическим многочленом уравнения (4). В том случае, когда он не имеет кратных корней, совокупность всех решений уравнения (4) описывается следующей теоремой.
Теорема 4. Предположим, что характеристический многочлен  уравнения
уравнения
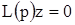 (6)
(6)
(см. (1) и (4)) не имеет кратных корней, и обозначим его корни через

Положим:
 (7)
(7)
Тогда при любых комплексных постоянных  функция
функция
 (8)
(8)
является решением уравнения (6). Решение это является общим в том смысле, что каждое решение уравнении (6) может быть получено по формуле (8) при надлежащем выборе констант 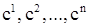 . При этом константы
. При этом константы  (называемые постоянными интегрирования) однозначно определяются для каждого данного решения z.
(называемые постоянными интегрирования) однозначно определяются для каждого данного решения z.
Заметим, что функции (7) определены на всей числовой прямой  .
.
Примеры
1. Найдем все комплексные решения уравнения

Его можно записать в виде (6), где

Непосредственно проверяется, что р = - 1 есть корень характеристического многочлена L(р). Разделив L(р) на р+1, получаем:

откуда находим еще два корня  . Таким образом, корнями многочлена L(р) являются числа
. Таким образом, корнями многочлена L(р) являются числа

В силу теоремы 4 общее комплексное решение рассматриваемого уравнения имеет вид:
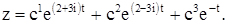
2. Будем считать, что система решений (7) удовлетворяет условиям
 (9)
(9)
и положим:

где  - действительные функции. Будем, далее, считать, что числа
- действительные функции. Будем, далее, считать, что числа  удовлетворяют условиям
удовлетворяют условиям
 (10)
(10)
и положим:

где 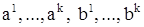 — действительные числа. При этих обозначениях общее действительное решение уравнения (6) записывается в виде:
— действительные числа. При этих обозначениях общее действительное решение уравнения (6) записывается в виде:

где

суть произвольные действительные числа.
|
из
5.00
|
Обсуждение в статье: Линейное однородное уравнении с постоянными коэффициентами (случай простых корней) |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

