 |
Главная |
Отметим, что в данном случае
|
из
5.00
|
 (10)
(10)
В случае решений (9) особая точка называется устойчивым узлом (рис.9 а). Говорят, что точка, неограниченно приближается к особой точке при 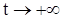 .
.
II. Корни характеристического уравнения действительные, положительные, различные:  . В этом случае решения выражаются также формулами (8) и соответственно (9). Но в данном случае при как угодно малых
. В этом случае решения выражаются также формулами (8) и соответственно (9). Но в данном случае при как угодно малых 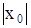 и
и 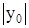 будет
будет 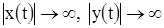 при
при 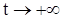 , так как
, так как 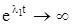 и
и 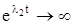 при
при 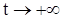 . На фазовой плоскости особая точка – неустойчивый узел: при
. На фазовой плоскости особая точка – неустойчивый узел: при 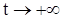 точка на траектории удаляется от точки покоя х = 0, у = 0 (рис. 9 б).
точка на траектории удаляется от точки покоя х = 0, у = 0 (рис. 9 б).
III. Корни характеристического уравнения действительные, разных знаков, например, 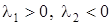 . Из формул (9) следует, что при как угодно малых
. Из формул (9) следует, что при как угодно малых 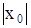 и
и 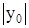 , если
, если 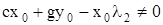 , будет
, будет 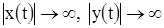 при
при 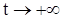 . Решение неустойчиво. На фазовой плоскости особая точка называется седлом (рис. 10).
. Решение неустойчиво. На фазовой плоскости особая точка называется седлом (рис. 10).
IV. Корни характеристического уравнения комплексные с отрицательной действительной частью: 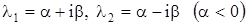 . Решение системы (4) будет
. Решение системы (4) будет
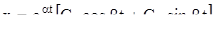
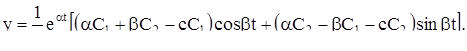 (11)
(11)
Если ввести обозначение
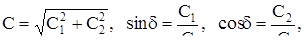
то уравнения (11) можно переписать в виде

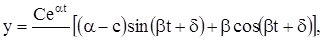 (12)
(12)
где 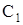 и
и 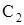 - произвольные постоянные, которые определяются из начальных условий
- произвольные постоянные, которые определяются из начальных условий 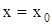 ,
, 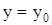 при t = 0, причем
при t = 0, причем
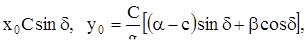
откуда находим
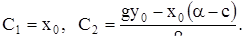 (13)
(13)
Снова заметим, что если g=0, то вид решения будет несколько иной, но характер анализа не изменится. Очевидно, что при любом 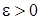 при достаточно малых
при достаточно малых 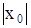 и
и 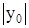 будут выполняться соотношения
будут выполняться соотношения
 .
.
Решение устойчиво. В данном случае при 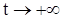
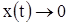 и
и 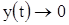 ,
,
неограниченное число раз меняя знаки. На фазовой плоскости особая точка называется устойчивым фокусом (рис. 13 а).
V. Корни характеристического уравнения комплексные с положительной действительной частью: 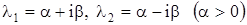 . В этом случае решение также выразится формулами (11), где
. В этом случае решение также выразится формулами (11), где 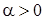 . При любых начальных условиях
. При любых начальных условиях 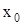 и
и 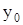
 и при
и при 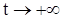 величины
величины 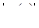 и
и 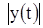 могут принимать как угодно большие значения. Решение неустойчиво. На фазовой плоскости особая точка называется неустойчивым фокусом. Точка по траектории неограниченно удаляется от начала координат (рис. 13 б).
могут принимать как угодно большие значения. Решение неустойчиво. На фазовой плоскости особая точка называется неустойчивым фокусом. Точка по траектории неограниченно удаляется от начала координат (рис. 13 б).
VI. Корни характеристического уравнения чисто мнимые: 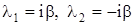 . Решение (11) в этом случае примут вид
. Решение (11) в этом случае примут вид

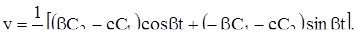 (14)
(14)
Постоянные 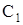 и
и 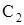 определяются по формулам (13):
определяются по формулам (13):
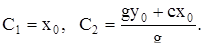 (15)
(15)
Очевидно, что при любом 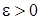 и при всех достаточно малых
и при всех достаточно малых 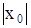 и
и 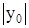 будет
будет  при любом t. Решение устойчиво. Здесь х и у – периодические функции от t.
при любом t. Решение устойчиво. Здесь х и у – периодические функции от t.
Чтобы произвести анализ интегральных кривых на фазовой плоскости, целесообразно первое из решений (14) записать в в следующем виде (см. (12)):
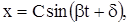
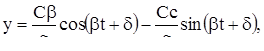 (16)
(16)
где С, 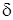 - произвольные постоянные. Из выражений (16) следует, что х и у – периодические функции от t. Исключаем параметр t из уравнений (16):
- произвольные постоянные. Из выражений (16) следует, что х и у – периодические функции от t. Исключаем параметр t из уравнений (16):
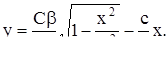
Освобождаясь от радикала, получим
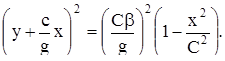 (17)
(17)
Это семейство кривых 2-го порядка (кривые действительные), зависящих от произвольной постоянной С. Каждая из них не имеет неограниченно удаленных точек. Следовательно, это семейство эллипсов, окружающих начало координат (при с=0 оси эллипсов параллельны осям координат). Особая точка называется центром (рис. 14).
VII. Пусть 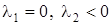 . Решение (8) в этом случае принимает вид
. Решение (8) в этом случае принимает вид
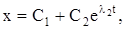
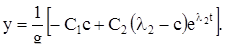 (18)
(18)
Очевидно, что при любом 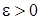 и при достаточно малых
и при достаточно малых 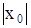 и
и 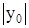 будет
будет  , при t > 0. Следовательно, решение устойчиво.
, при t > 0. Следовательно, решение устойчиво.
VIII. Пусть 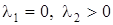 . Из формул (18) или (8’) следует, что решение неустойчиво, так как
. Из формул (18) или (8’) следует, что решение неустойчиво, так как 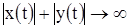 при
при 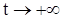 .
.
IX. Пусть 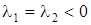 . Решение будет
. Решение будет

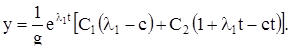 (19)
(19)
Так как 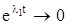 и
и 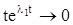 при
при 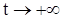 , то для любого
, то для любого 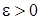 можно подобрать
можно подобрать 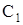 и
и 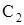 такие (путем выбора
такие (путем выбора 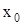 и
и 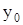 ), что будет
), что будет 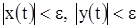 при любом t > 0. Следовательно, решение устойчиво. При этом
при любом t > 0. Следовательно, решение устойчиво. При этом 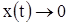 и
и 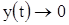 при
при 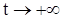 .
.
Заметим, что в случае 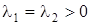 форма решения (18) сохраняется, но при
форма решения (18) сохраняется, но при 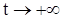
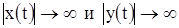 .
.
Решение неустойчиво.
X. Пусть 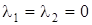 . Тогда
. Тогда
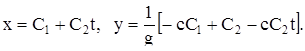 (20)
(20)
Откуда видно, что 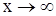 и
и 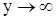 при
при 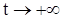 . Решение неустойчиво.
. Решение неустойчиво.
Чтобы дать общий критерий устойчивости решения системы (4), поступим следующим образом.
Запишем корни характеристического уравнения в форме комплексных чисел:
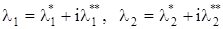
(в случае действительных корней 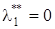 и
и 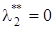 ).
).

Возьмем плоскость 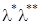 комплексной переменной и будем изображать корни характеристического уравнения точками на этой плоскости. Тогда на основании рассмотренных случаев условие устойчивости решения системы (4) можно сформулировать следующим образом.
комплексной переменной и будем изображать корни характеристического уравнения точками на этой плоскости. Тогда на основании рассмотренных случаев условие устойчивости решения системы (4) можно сформулировать следующим образом.
Если ни один из корней 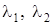 характеристического уравнения (6) не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво; если же хотя бы один корень лежит справа от мнимой оси или оба корня равны нулю, то решение неустойчив (рис.19).
характеристического уравнения (6) не лежит справа от мнимой оси, причем хотя бы один корень отличен от нуля, то решение устойчиво; если же хотя бы один корень лежит справа от мнимой оси или оба корня равны нулю, то решение неустойчив (рис.19).
А.М. Ляпунов исследовал вопрос об устойчивости решений систем уравнений при довольно общих предположениях относительно вида этих уравнений.
В теории колебаний часто рассматривают уравнение
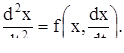 (21)
(21)
Обозначим
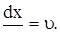 (22)
(22)
Тогда получаем систему уравнений
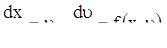 (23)
(23)
Фазовой плоскостью для этой системы будет плоскость 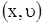 . Траектории на фазовой плоскости дают геометрическое изображение зависимости скорости
. Траектории на фазовой плоскости дают геометрическое изображение зависимости скорости 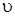 от координаты х и наглядно качественно характеризуют изменение х и
от координаты х и наглядно качественно характеризуют изменение х и 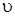 . Если точка х = 0,
. Если точка х = 0, 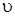 = 0 является особой точкой, то она определяет положение равновесия.
= 0 является особой точкой, то она определяет положение равновесия.
Так, например, если особая точка системы уравнений есть центр, т. е. Траектории на фазовой плоскости представляют собой замкнутые линии, окружающие начало координат, то движения определяемые уравнением (21), - незатухающие колебательные движения. Если особая точка фазовой плоскости есть фокус (при этом 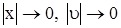 при
при 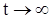 ), то движения, определяемые уравнением (21), - затухающие колебания. Если особая точка есть узел или седло (и это единственная особая точка), то
), то движения, определяемые уравнением (21), - затухающие колебания. Если особая точка есть узел или седло (и это единственная особая точка), то 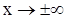 при
при 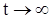 . В этом случае движущаяся материальная точка уходит в бесконечность.
. В этом случае движущаяся материальная точка уходит в бесконечность.
Если уравнение (21) линейное вида 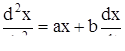 , то система (23) имеет вид
, то система (23) имеет вид
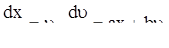
Это система вида (4). Точка х = 0, 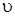 = 0 есть особая точка, она определяет положение равновесия. Отметим, что переменная ч – не обязательно механическое перемещение точки. Она может иметь различный физический смысл, например, обозначать величину, характеризующую электрические колебания.
= 0 есть особая точка, она определяет положение равновесия. Отметим, что переменная ч – не обязательно механическое перемещение точки. Она может иметь различный физический смысл, например, обозначать величину, характеризующую электрические колебания.
|
из
5.00
|
Обсуждение в статье: Отметим, что в данном случае |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

