 |
Главная |
Случай простых корней характеристического уравнения
|
из
5.00
|
А) Система дифференциальных уравнений (1) в векторной форме переписывается в виде:
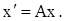 (2)
(2)
Здесь 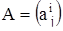 , а вместо системы
, а вместо системы 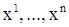 неизвестных функций введен неизвестный вектор
неизвестных функций введен неизвестный вектор
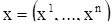 ;
;
под производной 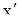 вектора х понимается вектор
вектора х понимается вектор 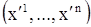 . Если h есть собственный вектор матрицы А с собственным значением
. Если h есть собственный вектор матрицы А с собственным значением 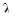 т.е. если
т.е. если
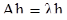
то векторная функция х, определяемая соотношением
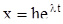 ,
,
является решением уравнения (2).
Последнее утверждение проверяется путем подстановки 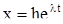 в соотношение (2).
в соотношение (2).
Теорема 8. Пусть
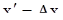 (3)
(3)
- такая система дифференциальных уравнений (см. А.)), что собственные значения 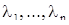 матрицы А попарно различны, и пусть
матрицы А попарно различны, и пусть
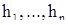
- соответствующие собственные векторы этой матрицы. Положим:
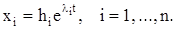 (4)
(4)
Тогда векторная функция
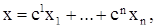 (5)
(5)
где 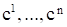 – константы, является решением уравнения (3), и всякое решение уравнения (3) задается этой формулой.
– константы, является решением уравнения (3), и всякое решение уравнения (3) задается этой формулой.
Доказательство. В силу предложения А) каждая функция 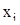 представляет собой решение уравнения (3), и потому в силу предложения А) §4 формула (5) всегда дает решение уравнения (3). Докажем теперь, что всякое решение уравнения (3) может быть записано в виде (5). Пусть
представляет собой решение уравнения (3), и потому в силу предложения А) §4 формула (5) всегда дает решение уравнения (3). Докажем теперь, что всякое решение уравнения (3) может быть записано в виде (5). Пусть 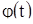 - произвольное решение уравнения (3). В силу теоремы 3 решение
- произвольное решение уравнения (3). В силу теоремы 3 решение 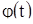 можно считать заданным на всей бесконечной прямой
можно считать заданным на всей бесконечной прямой 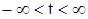 . Таким образом, решение это определено и при t = 0. Положим
. Таким образом, решение это определено и при t = 0. Положим 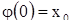 . Пусть
. Пусть
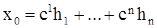
- разложение вектора 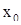 по векторам базиса
по векторам базиса 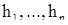 . Тогда решение х, определяемое формулой (5), очевидно, удовлетворяет начальным условиям
. Тогда решение х, определяемое формулой (5), очевидно, удовлетворяет начальным условиям
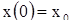
Тем же начальным условиям 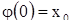 удовлетворяет и решение
удовлетворяет и решение 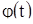 ; таким образом, в силу теоремы единственности (см. теорему 2),
; таким образом, в силу теоремы единственности (см. теорему 2), 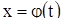 .
.
Итак, теорема 8 доказана.
В случае, если матрица 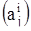 , задающая уравнение (3), действительна, перед нами встает задача выделения из всех решений (5) действительных решений.
, задающая уравнение (3), действительна, перед нами встает задача выделения из всех решений (5) действительных решений.
Б) Будем считать, что матрица 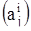 , задающая уравнение (3), действительна, и выберем векторы
, задающая уравнение (3), действительна, и выберем векторы 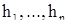 таким образом, чтобы действительным собственным значениям соответствовали действительные векторы, а комплексно сопряженным – комплексно сопряженные. Тогда в системе решений (4) каждому действительному собственному значению будет соответствовать действительное решение, а каждым двум комплексно сопряженным собственным значениям будут соответствовать комплексно сопряженные решения. Оказывается, что решение (5) тогда и только тогда действительно, когда константы, стоящие при действительных решениях, действительны, а константы, стоящие при комплексно сопряженных решениях, сопряжены.
таким образом, чтобы действительным собственным значениям соответствовали действительные векторы, а комплексно сопряженным – комплексно сопряженные. Тогда в системе решений (4) каждому действительному собственному значению будет соответствовать действительное решение, а каждым двум комплексно сопряженным собственным значениям будут соответствовать комплексно сопряженные решения. Оказывается, что решение (5) тогда и только тогда действительно, когда константы, стоящие при действительных решениях, действительны, а константы, стоящие при комплексно сопряженных решениях, сопряжены.
Общий случай
Перейдем теперь к решению системы (1) в общем случае (матрица 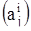 может иметь кратные собственные значения). Разбор этого случая опирается на весьма нетривиальную и сложно доказуемую алгебраическую теорему о приведении матрицы к жордановой форме.
может иметь кратные собственные значения). Разбор этого случая опирается на весьма нетривиальную и сложно доказуемую алгебраическую теорему о приведении матрицы к жордановой форме.
В) Запишем систему (1) в векторной форме
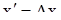 (6)
(6)
и пусть
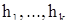
- некоторая серия с собственным значением 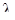 относительно матрицы А, так что выполнены соотношения
относительно матрицы А, так что выполнены соотношения
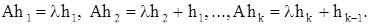
Введем последовательность векторных функций, положив:
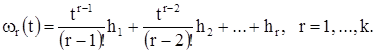 (7)
(7)
Оказывается тогда, что векторные функции
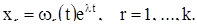 (8)
(8)
являются решениями уравнения (6), причем
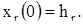 (9)
(9)
Таким образом, каждой серии из k векторов соответствует система из k решений.
Для доказательства того, что векторные функции (8) являются решениями уравнения (6), укажем два тождества относительно векторных функций (7). Тождества эти следующие:
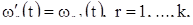
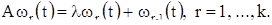
В этих соотношениях принято 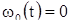 . Оба они проверяются непосредственно путем проведения элементарных вычислений. При помощи этих тождеств непосредственно проверяется, что функции (8) являются решениями уравнения (6). Действительно, мы имеем:
. Оба они проверяются непосредственно путем проведения элементарных вычислений. При помощи этих тождеств непосредственно проверяется, что функции (8) являются решениями уравнения (6). Действительно, мы имеем:
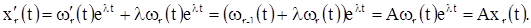
Перейдем теперь к формулировке и доказательству теоремы, дающей решение системы (1) в общем случае.
Теорема 9. Пусть
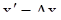 (10)
(10)
- векторная запись системы (1). Существует базис 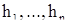 , состоящий из серий относительно матрицы А. Для определенности будем считать, что
, состоящий из серий относительно матрицы А. Для определенности будем считать, что 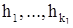 есть серия с собственным значением
есть серия с собственным значением 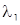 ;
; 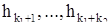 есть серия с собственным значением
есть серия с собственным значением 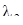 ; и т.д. В силу предложения В) каждой из серий соответствует система решений, так что мы можем выписать следующие решения уравнения (10):
; и т.д. В силу предложения В) каждой из серий соответствует система решений, так что мы можем выписать следующие решения уравнения (10):
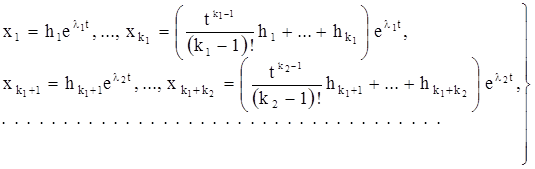 (11)
(11)
Оказывается, что формула
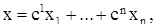 (12)
(12)
где 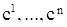 – константы, всегда дает решение уравнения (10) и что каждое решение уравнения (10) описывается формулой (12).
– константы, всегда дает решение уравнения (10) и что каждое решение уравнения (10) описывается формулой (12).
Доказательство. Так как функции 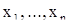 являются решениями уравнения (10) (см. В)), то в силу предложения А) §4 формула (12) всегда дает решение уравнения (10). Покажем, что всякое решение уравнения (10) при надлежащем подборе констант
являются решениями уравнения (10) (см. В)), то в силу предложения А) §4 формула (12) всегда дает решение уравнения (10). Покажем, что всякое решение уравнения (10) при надлежащем подборе констант 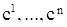 записывается в виде (12). Пусть
записывается в виде (12). Пусть 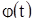 - произвольное решение уравнения (10). В силу теоремы 3 решение
- произвольное решение уравнения (10). В силу теоремы 3 решение 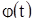 можно считать заданным на всей прямой
можно считать заданным на всей прямой 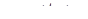 , и потому вектор
, и потому вектор 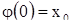 определен. Разложим этот вектор по базису
определен. Разложим этот вектор по базису 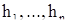 :
:
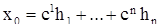
Если теперь подставить найденные константы 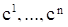 в соотношение (12), то мы получим решение
в соотношение (12), то мы получим решение 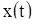 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям
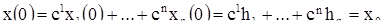
(см. (9)). Таким образом, решения 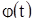 и
и 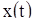 имеют общие начальные значения и потому совпадают.
имеют общие начальные значения и потому совпадают.
Итак, теорема 9 доказана.
Теперь нам осталось выделить из решений, заданных формулой (12), действительные решения в случае, когда матрица 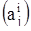 действительна. Делается это совершенно так же, как и в случае простых корней характеристического уравнения.
действительна. Делается это совершенно так же, как и в случае простых корней характеристического уравнения.
|
из
5.00
|
Обсуждение в статье: Случай простых корней характеристического уравнения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

