Формулировка теоремы существования и единственности

 

В §1 было рассмотрено одно дифференциальное уравнение первого порядка, причем была сформулирована теорема существования и единственности для этого уравнения. Теория обыкновенных дифференциальных уравнений имеет дело и с более общими системами уравнений. Обычно система обыкновенных дифференциальных уравнений состоит из стольких уравнений, сколько в нее входит неизвестных функций; при этом все неизвестные функции являются функциями одного и того же независимого переменного. Во всех случаях теорема существования и единственности является основным теоретическим положением, дающим возможность подойти к изучению данной системы дифференциальных уравнений.

Теорема существовании и единственности формулируется и доказывается применительно к системе уравнений, по внешнему виду имеющей несколько частный тип. В действительности же к этой системе уравнений сводятся системы сравнительно общего типа. Системы дифференциальных уравнений того частного тина, о котором здесь идет речь, мы будем называть в дальнейшем нормальными.

Система

 

 (1)

 

обыкновенных дифференциальных уравнений называется нормальной. В этой системе t —независимое переменное, 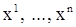— неизвестные функции; этого переменного, а  — функции от  переменных, заданные на некотором открытом множестве Г пространства размерности , в котором координатами точки являются числа . В дальнейшем всегда будет предполагаться, что функции

 

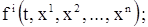
 (2)

 

непрерывны на открытом множестве Г; точно так же будет предполагаться, что и их частные производные

 

 (3)

 

существуют и непрерывны на множестве Г. Следует заметить, что частные производные (3), непрерывность которых предполагается, берутся только по переменным 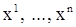, а не по независимому переменному t.

Решением системы уравнений (1) называется система непрерывных функций

 

,  (4)

 

определенных на некотором интервале  и удовлетворяющих системе (1). Интервал 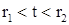 называется интервалом определения решения (4) (случаи ,  не исключаются). Считается, что система функций (4) удовлетворяет системе уравнений (1), если при подстановке в соотношение (1) вместо  функций (4) соотношения (1) превращаются в тождества по t на всем интервале . Для возможности этой подстановки необходимо, чтобы функции (4) имели производные в каждой точке интервала  и чтобы правые части уравнений (1) были определены для всех подставляемых в них значений аргументов. Таким образом, точка с координатами

 

 

должна принадлежать, множеству Г для всех значений t на интервале .

Дадим теперь формулировку теоремы существовании и единствен­ности для нормальной системы (1). (Доказательство будет приведено в § 13.)

Теорема 2. Пусть (1) — нормальная система обыкновенных дифференциальных уравнений. Здесь правые части уравнений (1) определены на некотором открытом множестве Г, а функции (2) и (3) непрерывны на этом множестве. Оказывается, что для каждой точки

 

 (5)

 

множества Г существует решение

 

,  (6)

 

системы (1), определенное на некотором интервале, содержащем точку , и удовлетворяющее условиям:

 

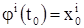;  (7)

 

Далее, оказывается, что если имеются два каких-либо решения

 (8)

 

системы (1), удовлетворяющих условиям

 

 (9)

 

причем каждое решение определено на своем собственном  интервале значений переменного t, содержащем точку  то решения эти совпадают всюду, где они оба определены.

Значения (5) называются начальными для решения (6), а соотношения (7) называются начальными условиями для этого решения. Мы будем говорить в дальнейшем, что решение (6) имеет начальные значения (5) или удовлетворяет начальным условиям (7).

Таким образом, теорему существования и единственности для нормальной системы кратко можно формулировать так:

Каковы бы ни были начальные значения (5), всегда существует решение системы (1) с этими начальными значениями, определенное на некотором интервале, содержащем точку . Далее, если имеются два решения с одинаковыми начальными значениями (5), каждое из которых определено на своем интервале, содержащем , то эти решения совпадают на общей части этих интервалов.

Введем здесь понятие непродолжаемого решения.

А) Пусть

 

,  (10)

 

- решение системы уравнений (1), определенное на интервале , и

 

,  (11)

 

- решение той же системы уравнений (1), определенное на интервале . Мы будем говорить, что решение (11) является продолжением решения (10), если интервал содержит интервал 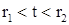(т.е. ) и решение (10) совпадает с решением (11) на интервале . В частности, мы будем считать, что решение (11) является продолжением решения (10) и в том случае, когда оба решения полностью совпадают, т. е. . Решение (10) будем называть непродолжаемым, если не существует никакого отличного от него решения, являющегося его продолжением.

Сформулируем теперь еще одну теорему существования.

Теорема 3. Пусть

 

 (12)

 

- нормальная линейная система уравнений. Здесь коэффициенты  и свободные члены 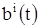 являются непрерывными функциями независимого переменного i, определенными на некотором интервале . Оказывается, что для любых начальных значений

 

 (13)

 

существует решение системы (12) с этими начальными значениями, определенное на всем интервале .

В частности, если коэффициенты и свободные члены системы (12) определены на всей прямой, т. е. если , то для любых начальных значений существует решение системы (12), определенное на всем бесконечном интервале .

Решения нормальной системы (1) интерпретируются геометрически в виде интегральных кривых (n+1)-мерном пространстве с координатами . Уравнения интегральной кривой имеют вид:

 

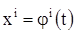,  (14)

 

где (14) есть решение системы.

Сама система (1) интерпретируется с помощью поля  направлений в (n+1)-мерном пространстве.

Примеры

1. Решим нормальную линейную систему уравнений

 

 (15)

 

Множеством Г для нее является все трехмерное пространство с координатами 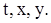 Непосредственно проверяется, что система функций

 

 (16)

 

где  и — произвольные постоянные, представляет собой решение системы (15). Для того чтобы попадать, что, выбирая надлежащим образом постоянные  и , можно получить по формуле (16) произвольное решение, зададимся начальными значениями 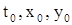 покажем, что среди решений (16) имеется решение с этими начальными значениями. Мы получаем для постоянных  и  условия

 

 (17)

 

Пусть  и  - полярные координаты точки , так что

 

 

Тогда уравнения (17) переписываются в виде:

 

 

Полагая

 

 

мы, очевидно, выполним условия (17). Таким образом, через каждую точку  проходит решение, задаваемое формулой (16).

В силу теоремы 2 (единственность) формула (16) охватывает совокупность всех решений.

2. Покажем, что если правые части (2) системы уравнений (1) k раз непрерывно дифференцируемы, т. е. имеют непрерывные производные порядка k (включая смешанные) по всем переменным , то (k+1)-я производная решения (4) системы (1) существует и непрерывна.

В самом деле, для решения (4) имеет место тождество:

 (18)

 

Если правые части (2) имеют непрерывные первые производные, то правая часть тождества (18) имеет непрерывную производную по t, и потому функция  существует и непрерывна. Дифференцируя написанное тождество (18) k раз, мы последовательно убедимся в существовании и непрерывности всех производных порядков 2, 3,..., k+1 функций .