 |
Главная |
Доказательство теоремы 2
|
из
5.00
|
Так как точка 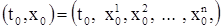 принадлежит открытому множеству Г, то существуют такие положительные числа q и a, что все точки
принадлежит открытому множеству Г, то существуют такие положительные числа q и a, что все точки 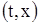 , удовлетворяющие условиям
, удовлетворяющие условиям
 , (14)
, (14)
лежат в множестве Г. Так как множество П, состоящее из всех точек 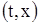 удовлетворяющих условиям (14), замкнуто и ограничено (рис.18), то. непрерывные функции
удовлетворяющих условиям (14), замкнуто и ограничено (рис.18), то. непрерывные функции
 и
и  ,
, 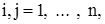
ограничены на нем, т. е. существуют такие положительные числа М и К, что
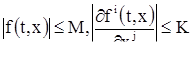 ,
, 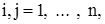 (15)
(15)
на множестве П.
Наряду с множеством П рассмотрим содержащееся в нем множество  определяемое неравенствами
определяемое неравенствами
 ,
,
где
 (16)
(16)
(рис. 18). Обозначим через  семейство всех непрерывных векторных функций, заданных на отрезке
семейство всех непрерывных векторных функций, заданных на отрезке  , графики которых проходят в
, графики которых проходят в  . Таким образом, функция
. Таким образом, функция 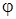 , определенная на отрезке
, определенная на отрезке  , тогда и только тогда принадлежит семейству
, тогда и только тогда принадлежит семейству  когда
когда

Рис. 18.
для любого t, принадлежащего этому отрезку, выполнено неравенство
 (17)
(17)
Постараемся выбрать теперь число r таким образом, чтобы были выполнены следующие два условия:
а) Если функция 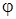 принадлежит семейству
принадлежит семейству  , то функция
, то функция  (см. (10), (11)) также принадлежит семейству
(см. (10), (11)) также принадлежит семейству  .
.
б) Существует такое число  , что для любых двух функций
, что для любых двух функций  семейства
семейства  , имеет место неравенство
, имеет место неравенство
 (18)
(18)
Рассмотрим условие а). Для того чтобы функция  принадлежала семейству
принадлежала семейству  , необходимо и достаточно, чтобы при
, необходимо и достаточно, чтобы при  было выполнено неравенство:
было выполнено неравенство:
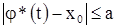 .
.
В силу (10), (5) и (15) мы имеем:
 .
.
Из этого видно, что при
 (19)
(19)
условие а) выполнено.
Рассмотрим теперь условие б). Мы имеем:
 . (20)
. (20)
Оценим теперь последнее подынтегральное выражение, пользуясь неравенствами (6) и (15):
 . (21)
. (21)
Из (20) и (21) следует

Таким образом, условие б) выполнено, если
 , (22)
, (22)
где  .
.
Итак, если число r удовлетворяет неравенствам (16), (19), (22) (которые мы в дальнейшем будем считать выполненными), то для семейства  выполнены условия а) и б).
выполнены условия а) и б).
Построим теперь последовательность векторных функций
 ,
, 
 (23)
(23)
определенных на отрезке  , положив
, положив
 (24)
(24)
Так как функция  принадлежит семейству
принадлежит семейству  , то и все функции последовательности (23) принадлежат этому же семейству (см. условие а)). Далее, мы имеем (см. (17)):
, то и все функции последовательности (23) принадлежат этому же семейству (см. условие а)). Далее, мы имеем (см. (17)):

В силу (18) получаем:
 ,
,
отсюда
 . (25)
. (25)
Таким образом, в силу В) последовательность (23) равномерно сходится к некоторой непрерывной функции 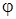 , принадлежащей семейству
, принадлежащей семейству  . Покажем, что функция
. Покажем, что функция 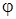 удовлетворяет уравнению (12). Для этого заметим, что последовательность
удовлетворяет уравнению (12). Для этого заметим, что последовательность

Равномерно сходится к функции  ; действительно, мы имеем (см. (18))
; действительно, мы имеем (см. (18))
 .
.
Переходя в соотношении (24) к приделу при  , получаем:
, получаем:
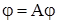 .
.
Итак, существование решении 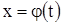 уравнения (3), удовлетворяющего начальному условию (8), доказано; при этом установлено, что решение
уравнения (3), удовлетворяющего начальному условию (8), доказано; при этом установлено, что решение 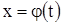 определено на интервале
определено на интервале  , где r – произвольное число; удовлетворяющее неравенствам (16), (19), (22).
, где r – произвольное число; удовлетворяющее неравенствам (16), (19), (22).
Перейдем теперь к доказательству единственности. Пусть  и
и  - два решения уравнения (3) с общими начальными значениями
- два решения уравнения (3) с общими начальными значениями 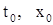 и
и 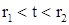 — интервал, являющийся пересечением интервалов существования решений
— интервал, являющийся пересечением интервалов существования решений  и
и  ; очевидно, что
; очевидно, что  . Покажем, что если решения
. Покажем, что если решения 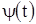 и
и  совпадают в некоторой точке
совпадают в некоторой точке 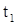 интервала
интервала 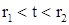 , то они совпадают и на некотором интервале
, то они совпадают и на некотором интервале  , где r – достаточно малое положительное число. Положим
, где r – достаточно малое положительное число. Положим  ; тогда величины
; тогда величины 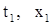 могут быть приняты за начальные значения обоих решений
могут быть приняты за начальные значения обоих решений  и
и  . В этом смысле точка
. В этом смысле точка  ничем не отличается от точки
ничем не отличается от точки  и потому мы сохраним за точкой
и потому мы сохраним за точкой  обозначение
обозначение  ; это позволит нам сохранить и другие прежние, обозначения. Переходя от дифференциального уравнения (3) к интегральному уравнению (9), мы получаем для обеих функций
; это позволит нам сохранить и другие прежние, обозначения. Переходя от дифференциального уравнения (3) к интегральному уравнению (9), мы получаем для обеих функций 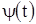 и
и  интегральные равенства, которые в операторной форме могут быть записаны в виде:
интегральные равенства, которые в операторной форме могут быть записаны в виде:
 . (26)
. (26)
Выберем теперь, как и прежде, в множестве Г множество П с центром в точке  (см, неравенства (14)), содержащееся в Г, а затем множество
(см, неравенства (14)), содержащееся в Г, а затем множество  таким образом, чтобы число r, кроме неравенств (16), (19), (22), удовлетворяло еще тому условию, что при
таким образом, чтобы число r, кроме неравенств (16), (19), (22), удовлетворяло еще тому условию, что при  функции
функции  и
и  определены и удовлетворяют неравенствам:
определены и удовлетворяют неравенствам:
 ,
,  .
.
Это возможно, так как функции 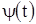 и
и  непрерывны. Тогда функции
непрерывны. Тогда функции 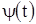 и
и  , рассматриваемые на, отрезке
, рассматриваемые на, отрезке  , входят в семейство
, входят в семейство  и, следовательно, в силу неравенства (18) и соотношений (26), получаем:
и, следовательно, в силу неравенства (18) и соотношений (26), получаем:
 ,
,
а это возможно только тогда, когда  , т.е. когда функций
, т.е. когда функций  и
и  совпадают на отрезке
совпадают на отрезке  .
.
Докажем теперь, что функции 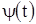 и
и  совпадают на всем интервале
совпадают на всем интервале 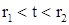 . Допустим противоположное, именно, что существует точка
. Допустим противоположное, именно, что существует точка  интервала
интервала 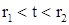 , для которой
, для которой  . Ясно, что
. Ясно, что  . Для определенности будем считать, что
. Для определенности будем считать, что  . Обозначим через N множество всех тех точек
. Обозначим через N множество всех тех точек 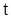 отрезка
отрезка  , для которых
, для которых  , и докажем, что множество N замкнуто. В самом деле, пусть
, и докажем, что множество N замкнуто. В самом деле, пусть 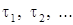 — последовательность точек множества N, сходящаяся к некоторой точке
— последовательность точек множества N, сходящаяся к некоторой точке  . Тогда
. Тогда  , и потому, в силу непрерывности функций
, и потому, в силу непрерывности функций  и
и  ,
,
 ,
,
т.е. точка  также принадлежит множеству N.
также принадлежит множеству N.
Обозначим через 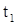 точную верхнюю грань множества N. Так как N замкнуто, то
точную верхнюю грань множества N. Так как N замкнуто, то 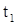 принадлежит этому множеству, т. е
принадлежит этому множеству, т. е  ; следовательно,
; следовательно,  . Но тогда, в силу ранее доказанного, функции
. Но тогда, в силу ранее доказанного, функции 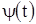 и
и  должны совпадать на некотором интервале
должны совпадать на некотором интервале  , и точка
, и точка 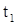 не может быть точной верхней гранью множества N. Таким образом, мы пришли к противоречию.
не может быть точной верхней гранью множества N. Таким образом, мы пришли к противоречию.
Итак, теорема 2 доказана.
|
из
5.00
|
Обсуждение в статье: Доказательство теоремы 2 |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

